Sample bartleby Q&A Solution
You ask questions, our tutors answer
Browse
Question
Why is binary search algorithm better than sequential search?
Expert Answer
- Sequential search algorithm involves visiting each and every element of the list of elements and see if the matching element is found in the list. This implies that every element is a candidate element. It can in the worst case take n searches if there are n elements in the list.
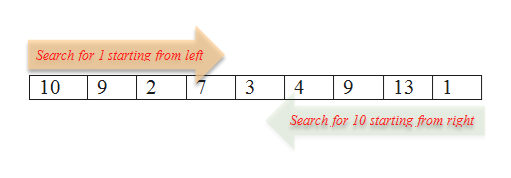
- For example, in the list below if search is made for 1 and if the search is started from the left end then it will take 9 search steps to find the match. If the search is made from the right then it is a lucky scenario and it just takes one step.
- But again if we decide to search for element 10 and we decided to search from right then it will again take 9 steps. These are extreme cases but the point is that the worst case scenario if n searches for n elements.
- For binary search to work the elements should be ordered (sorted) in ascending or descending order. Once we have the list or collection which has been sorted, the binary search algorithm is applied.
- The algorithm approaches the problem by dividing the search space into two portions at each stage and does further search in only one of the halves. As a result the total elements to be searched is aproximately halved in each stage.
- So if there are 100 elements, then in the first stage only one half is considered for the next stage, in the next stage 25 elements, around 12 elements in the third and so on. The algorithm hence takes approximately (log n) steps if there are n elements.
- How this halving approach works is explained in the next step.
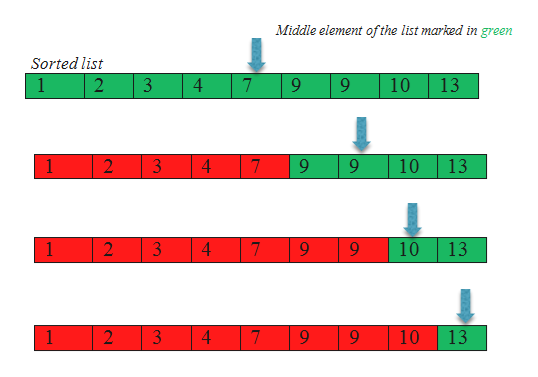
- At each stage the middle element is taken in the sorted list. So if there are 9 elements indexed from 0 to 8 (zero indexing assumed) then (0+8) / 2 = 4. Hence the element with index 4 is chosen as the middle element which is 7. It is compared with the element to be searched say 13.
- Since, 7 < 13 so it is not necessary to search for elements lesser than the seventh element. We proceed accordingly as shown in the diagram. Next stage middle element is found by taking the elements from index 5 to 8, i.e. (5+8) / 2 = 6.5 => 6. Sixth element is 9.
- Since 9 < 13 so it is not necessary to search for elements to the left of the sixth element. In the last stage the middle element is the eight element which matches the target element. So we stop here.
- The total steps taken is log 10 (to the base 2) which is 3.3 => 3 approximately.