Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
Bartleby Related Questions Icon

Related questions

Q: Find (u - 2v) · (2u – v), given that u · u = 5, u. v = 6, and v · v = 9. %3D
A:
Q: 230 Find AB or BA, whichever is possible.
A: Given  problem:-
Q: Studying
A: Given information: Sample size n=10 Sample mean x¯=38 minutes Sample standard deviation s=6 minutes…
Q: 2x₁ + 5x₂ +3x3 = -1 10 x₁ + 30x₂ +10x3 = 1 40x₁ + 10x₂ +30x3 = -8
A:
Q: Simplity b-[b-Ca+b) - CB-Cb-a-b)J+2a]
A:
Q: Find an SVD for [-3 1]
A: The given problem is to find the singular value decomposition for the given matrix. Given matrix is…
Q: curl(curl F)= grad(div F) - 2F
A:
Q: 4 x₁ +5x₂ +3 x3 = -27 2x₁ + 6x₂+2x3 = -15 2x₁ - x₂ + x3 = 12
A: The given system of linear equations, 4x1+5x2+3x3=-272x1+6x2+2x3=-152x1-x2+x3=12 We have to find…
Q: Long division
A: The given algebraic expression is: (2x5 – 4 x3 + 3 x2 + 5 x - 15) / (x2 - 5) Write the problem in…
Q: 22. x + y = 2x + 3y = 3 15
A: Solve the linear equations  13x+47y= 32x+3y= 15
Q: Linear algebra number 1 a and b show all work
A:
Q: Sx -1 xtan xdx
A: Solution of given question is written in below steps.
Q: ncos(5 Z)dz TU
A:
Q: -5 4 0 1 0 * 0 * 0 1 0. 0. . 1 0. 8. 0. 2 0.
A:
Q: linear algebra
A: 6. The given matrix is
Q: What is the dimension of the space spanned by 7. 3 3 1 6. 6 4 8. 0. 12
A:
Q: 14. 2x 8. 2x, 3x + 6x 2x
A:
Q: linear algebra   What does Span {v1,v2,v3} mean how  do I explain this
A: Solution:
Q: 1 2 x² +6x+18 -dx
A: A detailed solution is given below. We know that, ∫dx(x+a)2+a2 =  1a tan-1x+aa + c
Q: x² 2 =dx 2 √4+x²
A:
bartleby

Concept explainers

Equations and Inequations
Equations and inequalities describe the relationship between two mathematical expressions.
Linear Functions
A linear function can just be a constant, or it can be the constant multiplied with the variable like x or y. If the variables are of the form, x2, x1/2 or y2 it is not linear. The exponent over the variables should always be 1.
Question

Linear algebra

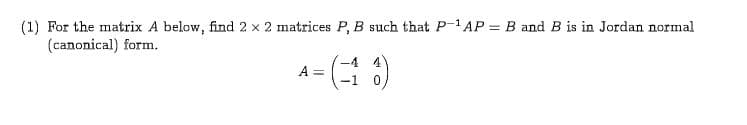
(1) For the matrix A below, find 2 x 2 matrices P, B such that P-1 AP (canonical) form. B and B is in Jordan normal -4 4 (0) A =
expand button
Transcribed Image Text:(1) For the matrix A below, find 2 x 2 matrices P, B such that P-1 AP (canonical) form. B and B is in Jordan normal -4 4 (0) A =
Expert Solution
Check Mark
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
bartleby
This is a popular solution
See solutionCheck out a sample Q&A here
Step 1
VIEW
Step 2
VIEW
Step 3
VIEW
Step 4
VIEW
bartleby

Trending nowThis is a popular solution!

bartleby

Step by stepSolved in 4 steps with 3 images

See solution
Check out a sample Q&A here
Blurred answer
Knowledge Booster
Background pattern image
Advanced Math
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.
Similar questions
Recommended textbooks for you
Text book image
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Text book image
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Text book image
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Text book image
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Text book image
Basic Technical Mathematics
Advanced Math
ISBN:9780134437705
Author:Washington
Publisher:PEARSON
Text book image
Topology
Advanced Math
ISBN:9780134689517
Author:Munkres, James R.
Publisher:Pearson,
SEE MORE TEXTBOOKS