23. If f(5) = 4, fi(5) = –1, g(5) = 2, and g/(5) = -3, find h/(5) for each of the following functions: f(x) iv) h(x) = (f(x))². g(x) i) h(x) = 2f(x)–3g(x) ii) h(x) = f(x)g(x) (iii) h(x) =
23. If f(5) = 4, fi(5) = –1, g(5) = 2, and g/(5) = -3, find h/(5) for each of the following functions: f(x) iv) h(x) = (f(x))². g(x) i) h(x) = 2f(x)–3g(x) ii) h(x) = f(x)g(x) (iii) h(x) =
Algebra: Structure And Method, Book 1
(REV)00th Edition
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Chapter11: Rational And Irrational Numbers
Section: Chapter Questions
Problem 23CLR
Related questions
Question
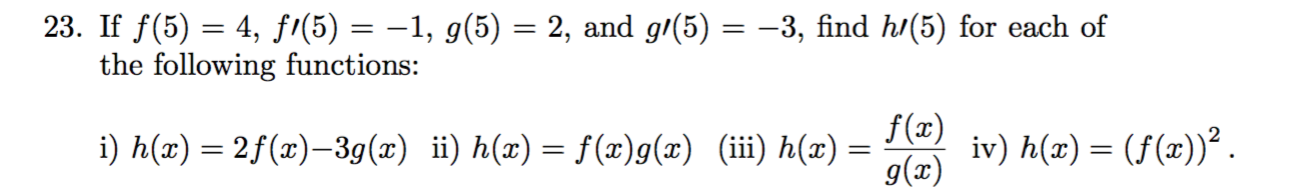
Transcribed Image Text:23. If f(5) = 4, fi(5) = –1, g(5) = 2, and g/(5) = -3, find h/(5) for each of
the following functions:
f(x)
iv) h(x) = (f(x))².
g(x)
i) h(x) = 2f(x)–3g(x) ii) h(x) = f(x)g(x) (iii) h(x) =
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 5 steps with 5 images

Recommended textbooks for you

Algebra: Structure And Method, Book 1
Algebra
ISBN:
9780395977224
Author:
Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:
McDougal Littell

College Algebra
Algebra
ISBN:
9781305115545
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning

Algebra: Structure And Method, Book 1
Algebra
ISBN:
9780395977224
Author:
Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:
McDougal Littell

College Algebra
Algebra
ISBN:
9781305115545
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:
9781305071742
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning