4. Suppose that (X, dx) and (Y, dy) are metric spaces, and define distance on X × Y by Prove that (Tmyn) → (z, y) in X × Y if and only ifFm → z in X and Un → y in Y. 5. If f:X → Y, the graph of f is the set G = {(x, f(x)) : x E X} X × Y. Suppose that f is a mapping of a compact metric space X into a metric space Y. Prove that f is continuous on X if and only if its graph G is compact. Hint: Use Exercise 4, and for the - part, also Exercise 3 applied in G.
4. Suppose that (X, dx) and (Y, dy) are metric spaces, and define distance on X × Y by Prove that (Tmyn) → (z, y) in X × Y if and only ifFm → z in X and Un → y in Y. 5. If f:X → Y, the graph of f is the set G = {(x, f(x)) : x E X} X × Y. Suppose that f is a mapping of a compact metric space X into a metric space Y. Prove that f is continuous on X if and only if its graph G is compact. Hint: Use Exercise 4, and for the - part, also Exercise 3 applied in G.
Elements Of Modern Algebra
8th Edition
ISBN:9781285463230
Author:Gilbert, Linda, Jimmie
Publisher:Gilbert, Linda, Jimmie
Chapter5: Rings, Integral Domains, And Fields
Section5.4: Ordered Integral Domains
Problem 8E: If x and y are elements of an ordered integral domain D, prove the following inequalities. a....
Related questions
Question
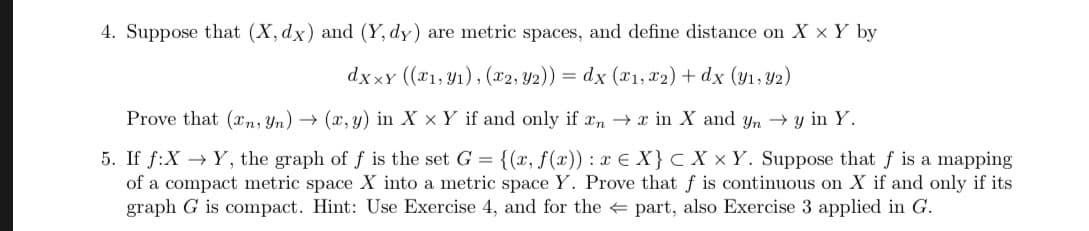
Transcribed Image Text:4. Suppose that (X, dx) and (Y, dy) are metric spaces, and define distance on X × Y by
Prove that (Tmyn) → (z, y) in X × Y if and only ifFm → z in X and Un → y in Y.
5. If f:X → Y, the graph of f is the set G = {(x, f(x)) : x E X}
X × Y. Suppose that f is a mapping
of a compact metric space X into a metric space Y. Prove that f is continuous on X if and only if its
graph G is compact. Hint: Use Exercise 4, and for the - part, also Exercise 3 applied in G.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 5 steps with 2 images

Recommended textbooks for you

Elements Of Modern Algebra
Algebra
ISBN:
9781285463230
Author:
Gilbert, Linda, Jimmie
Publisher:
Cengage Learning,

Elements Of Modern Algebra
Algebra
ISBN:
9781285463230
Author:
Gilbert, Linda, Jimmie
Publisher:
Cengage Learning,