4. Z F11 10 fleae Cung latly to tt StandandNsmel Num Pause 8 Len a tandand ma Cune uhdt Ahis aDaa +750 End Ins 9750 SO00 190 41 Remembn to pultracl Yong tae asond hal cadend in table Odds o Ceng mirdde Lotn deaimal and peacent Cod Knows nnd telt ALA Tuergi15 4;15 wed 1;00-40O Thu 154S ass The Cumulative Standardized Normal Distribution (continued) Entry represents area under the cumulative standardized normal distribution from -0o to Z 0 Z Cumulative Probabilities Z 0.00 0.01 0.02 0.09 0.03 0.08 0.04 0.05 0.06 0.07 0.5000 0.0 0.5040 0.5080 0.5359 0.5319 0.5120 0.5160 0.5279 0.5199 0.5239 0.1 0.5398 0.5438 0.5478 0.5753 0.5714 0.5517 0.5675 0.5557 0.5596 0.5636 0.2 0.5793 0.5832 0.6141 0.5871 0.6103 0.6064 0.5910 0.5948 0.5987 0.6026 0.3 0.6179 0.6217 0.6255 0.6628 0.6517 0.6480 0.6293 0.6443 0.6406 0.6331 0.6368 0.4 0.6554 0.6591 0.6879 0.6844 0.6664 0.6808 0.6700 0.6772 0.6736 0.6915 0.5 0.6950 0.7190 0.6985 0.7224 0.7019 0.7054 0.7157 0.7088 0.7123 0.6 0.7257 0.7291 0.7324 0.7549 0.7357 0.7389 0.7518 0.7486 0.7422 0.7454 0.7 0.7580 0.7612 0.7852 0.7642 0.7823 0.7673 0.7704 0.7734 0.7764 0.7794 .0.8 0.7881 0.7910 0.7939 0.8133 0.8106 0.7967 0.7995 0.8023 0.8051 0.8078 0.9 0.8159 0.8186 0.8212 0.8389 0.8238 0.8264 0.8365 0.8340 0.8289 0.8315 1.0 0.8413 0.8438 0.8461 0.8621 0.8508 0.8599 0.8485 0.8554 0.8577 0.8531 0.8665 1.1 0.8643 0.8686 0.8729 0.8708 0.8749 0.8790 0.8810 0.8830 0.8770 0.8925 0.8869 1.2 0.8849 0.8888 0.8907 0.8962 O.8980 0.9147 0.8997 0.8944 0.9015 0.9115 1.3 0.9066 0.9032 0.9049 0.9082 0.9099 0.9162 0.9131 0.9177 0.9207 1.4 0.9222 0.9236 0.9251 0.9192 0.9265 0.9279 0.9292 0.9306 0.9319 0.9382 0.9370 0.9394 0.9345 0.9357 0.9406 1.5 0.9332 0.9418 0.9429 0.9441 0.9484 0.9495 0.9463 0.9474 0.9505 0.9515 0.9525 1.6 0.9452 0.9535 0.9545 0.9591 0.9582 0.9599 0.9573 0.9616 0.9564 0.9608 0.9625 1.7 0.9554 0.9633 0.9664 0.9678 0.9671 0.9656 0.9686 0.9693 0.9641 0.9649 0.9699 1.8 0.9706 0.9732 0.9726 0.9738 0.9744 0.9750 0.9719 0.9756 0.9761 0.9713 1.9 0.9767 0.9798 0.9788 o3 0.9793 0.9803 0.9783 0.9808 0.9778 0.9812 0.9772 2.0 0.9817 0.9830 0.9834 0.9838 0.9842 0.9846 0.9826 0.9850 0.9854 0.9821 2.1 0.9857 0.9871 0.9875 0.9878 0.9881 0.9868 0.9864 0.9884 0.9887 0.9861 2.2 0.9890 0.9904 0.9906 0.9898 0.9901 0.9909 0.9896 0.9911 0.9893 0.9913 2.3 0.9916 0.9927 0.9929 0.9922 0.9925 0.9931 0.9932 0.9920 0.9918 0.9934 0.9936 2.4 0.9941 0.9945 0.9946 0.9943 0.9948 0.9949 0.9940 0.9938 0.9951 0.9952 2.5 0.9961 0.9960 0.9959 0.9956 0.9957 0.9962 0.9955 0.9953 0.9963 2.6 0.9964 0.9969 0.9970 0.9968 0.9967 0.9971 0.9972 0.9966 0.9965 0.9973 2.7 0.9974 0.9977 0.9977 0.9978 0.9976 0.9979 0.9975 0.9979 0.9974 0.9980 2.8 0.9981 0.9984 0.9983 0.9984 0.9982 0.9985 0.9982 0.9985 0.9981 0.9986 2.9 0.9986 0.99874 0.99878 0.99882 0.99886 0.99889 0.99869 0.99865 0.99893 0.99897 0.99900 3.0 0.99916 0.99910 0.99913 0.99918 0.99906 0.99921 0.99903 0.99924 0.99926 3.1 0.99929 0.99938 0.99936 0.99940 0.99942 0.99944 0.99934 0.99931 0.99946 0.99948 3.2 0.99950 0.99955 0.99960 0.99972 0.99957 0.99958 0.99961 0.99952 0.99953 0.99962 3.3 0.99964 0.99965 0.99970 0.99969 0.99971 0.99968 0.99966 0.99973 0.99981 0.99974 3.4 0.99975 0.99976 0.99979 0.99978 0.99980 0.99981 0.99978 0.99977 0.99982 3.5 0.99983 0.99983 0.99986 0.99985 0.99986 0.99987 0.99985 0.99987 0.99984 0.99988 3.6 0.99988 0.99989 0.99990 0.99991 0.99990 0.99991 0.99989 0.99990 0.99992 3.7 0.99992 0.99992 0.99992 0.99993 0.99994 0.99994 0.99994 0.99993 0.99993 0.99994 3.8 0.99995 0.99995 0.99995 0.99996 0.99996 0.99996 0.99995 0.99995 0.99996 0.99996 3.9 0.99996 0.99997 0.99997 0.999968329 4.0 Nagative .l Subhacr 0.999996602 4.5 Flip 0.999999713 5.0 0.999999981 0, 990 5.5 0.999999999 6.0 ./0a0 0.2 990 dont pant
4. Z F11 10 fleae Cung latly to tt StandandNsmel Num Pause 8 Len a tandand ma Cune uhdt Ahis aDaa +750 End Ins 9750 SO00 190 41 Remembn to pultracl Yong tae asond hal cadend in table Odds o Ceng mirdde Lotn deaimal and peacent Cod Knows nnd telt ALA Tuergi15 4;15 wed 1;00-40O Thu 154S ass The Cumulative Standardized Normal Distribution (continued) Entry represents area under the cumulative standardized normal distribution from -0o to Z 0 Z Cumulative Probabilities Z 0.00 0.01 0.02 0.09 0.03 0.08 0.04 0.05 0.06 0.07 0.5000 0.0 0.5040 0.5080 0.5359 0.5319 0.5120 0.5160 0.5279 0.5199 0.5239 0.1 0.5398 0.5438 0.5478 0.5753 0.5714 0.5517 0.5675 0.5557 0.5596 0.5636 0.2 0.5793 0.5832 0.6141 0.5871 0.6103 0.6064 0.5910 0.5948 0.5987 0.6026 0.3 0.6179 0.6217 0.6255 0.6628 0.6517 0.6480 0.6293 0.6443 0.6406 0.6331 0.6368 0.4 0.6554 0.6591 0.6879 0.6844 0.6664 0.6808 0.6700 0.6772 0.6736 0.6915 0.5 0.6950 0.7190 0.6985 0.7224 0.7019 0.7054 0.7157 0.7088 0.7123 0.6 0.7257 0.7291 0.7324 0.7549 0.7357 0.7389 0.7518 0.7486 0.7422 0.7454 0.7 0.7580 0.7612 0.7852 0.7642 0.7823 0.7673 0.7704 0.7734 0.7764 0.7794 .0.8 0.7881 0.7910 0.7939 0.8133 0.8106 0.7967 0.7995 0.8023 0.8051 0.8078 0.9 0.8159 0.8186 0.8212 0.8389 0.8238 0.8264 0.8365 0.8340 0.8289 0.8315 1.0 0.8413 0.8438 0.8461 0.8621 0.8508 0.8599 0.8485 0.8554 0.8577 0.8531 0.8665 1.1 0.8643 0.8686 0.8729 0.8708 0.8749 0.8790 0.8810 0.8830 0.8770 0.8925 0.8869 1.2 0.8849 0.8888 0.8907 0.8962 O.8980 0.9147 0.8997 0.8944 0.9015 0.9115 1.3 0.9066 0.9032 0.9049 0.9082 0.9099 0.9162 0.9131 0.9177 0.9207 1.4 0.9222 0.9236 0.9251 0.9192 0.9265 0.9279 0.9292 0.9306 0.9319 0.9382 0.9370 0.9394 0.9345 0.9357 0.9406 1.5 0.9332 0.9418 0.9429 0.9441 0.9484 0.9495 0.9463 0.9474 0.9505 0.9515 0.9525 1.6 0.9452 0.9535 0.9545 0.9591 0.9582 0.9599 0.9573 0.9616 0.9564 0.9608 0.9625 1.7 0.9554 0.9633 0.9664 0.9678 0.9671 0.9656 0.9686 0.9693 0.9641 0.9649 0.9699 1.8 0.9706 0.9732 0.9726 0.9738 0.9744 0.9750 0.9719 0.9756 0.9761 0.9713 1.9 0.9767 0.9798 0.9788 o3 0.9793 0.9803 0.9783 0.9808 0.9778 0.9812 0.9772 2.0 0.9817 0.9830 0.9834 0.9838 0.9842 0.9846 0.9826 0.9850 0.9854 0.9821 2.1 0.9857 0.9871 0.9875 0.9878 0.9881 0.9868 0.9864 0.9884 0.9887 0.9861 2.2 0.9890 0.9904 0.9906 0.9898 0.9901 0.9909 0.9896 0.9911 0.9893 0.9913 2.3 0.9916 0.9927 0.9929 0.9922 0.9925 0.9931 0.9932 0.9920 0.9918 0.9934 0.9936 2.4 0.9941 0.9945 0.9946 0.9943 0.9948 0.9949 0.9940 0.9938 0.9951 0.9952 2.5 0.9961 0.9960 0.9959 0.9956 0.9957 0.9962 0.9955 0.9953 0.9963 2.6 0.9964 0.9969 0.9970 0.9968 0.9967 0.9971 0.9972 0.9966 0.9965 0.9973 2.7 0.9974 0.9977 0.9977 0.9978 0.9976 0.9979 0.9975 0.9979 0.9974 0.9980 2.8 0.9981 0.9984 0.9983 0.9984 0.9982 0.9985 0.9982 0.9985 0.9981 0.9986 2.9 0.9986 0.99874 0.99878 0.99882 0.99886 0.99889 0.99869 0.99865 0.99893 0.99897 0.99900 3.0 0.99916 0.99910 0.99913 0.99918 0.99906 0.99921 0.99903 0.99924 0.99926 3.1 0.99929 0.99938 0.99936 0.99940 0.99942 0.99944 0.99934 0.99931 0.99946 0.99948 3.2 0.99950 0.99955 0.99960 0.99972 0.99957 0.99958 0.99961 0.99952 0.99953 0.99962 3.3 0.99964 0.99965 0.99970 0.99969 0.99971 0.99968 0.99966 0.99973 0.99981 0.99974 3.4 0.99975 0.99976 0.99979 0.99978 0.99980 0.99981 0.99978 0.99977 0.99982 3.5 0.99983 0.99983 0.99986 0.99985 0.99986 0.99987 0.99985 0.99987 0.99984 0.99988 3.6 0.99988 0.99989 0.99990 0.99991 0.99990 0.99991 0.99989 0.99990 0.99992 3.7 0.99992 0.99992 0.99992 0.99993 0.99994 0.99994 0.99994 0.99993 0.99993 0.99994 3.8 0.99995 0.99995 0.99995 0.99996 0.99996 0.99996 0.99995 0.99995 0.99996 0.99996 3.9 0.99996 0.99997 0.99997 0.999968329 4.0 Nagative .l Subhacr 0.999996602 4.5 Flip 0.999999713 5.0 0.999999981 0, 990 5.5 0.999999999 6.0 ./0a0 0.2 990 dont pant
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
Related questions
Question
Can I have this completed problem explained step by step it is complete but I need more info as to how to do it or how it was done on my paper using my chart as well
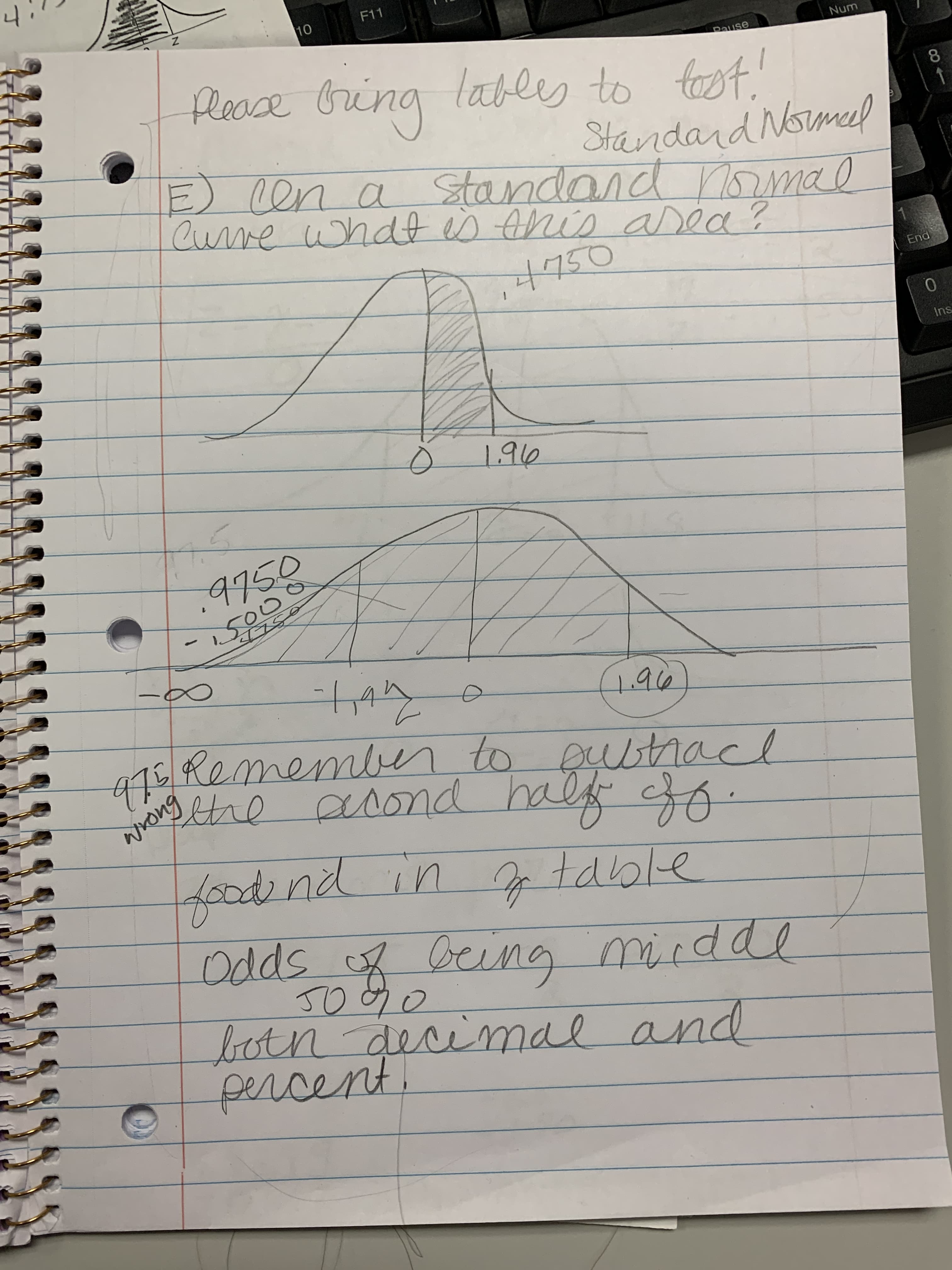
Transcribed Image Text:4.
Z
F11
10
fleae Cung
latly to tt
StandandNsmel
Num
Pause
8
Len a
tandand ma
Cune uhdt Ahis aDaa
+750
End
Ins
9750
SO00
190
41 Remembn to pultracl
Yong
tae asond hal
cadend in table
Odds o Ceng
mirdde
Lotn deaimal and
peacent
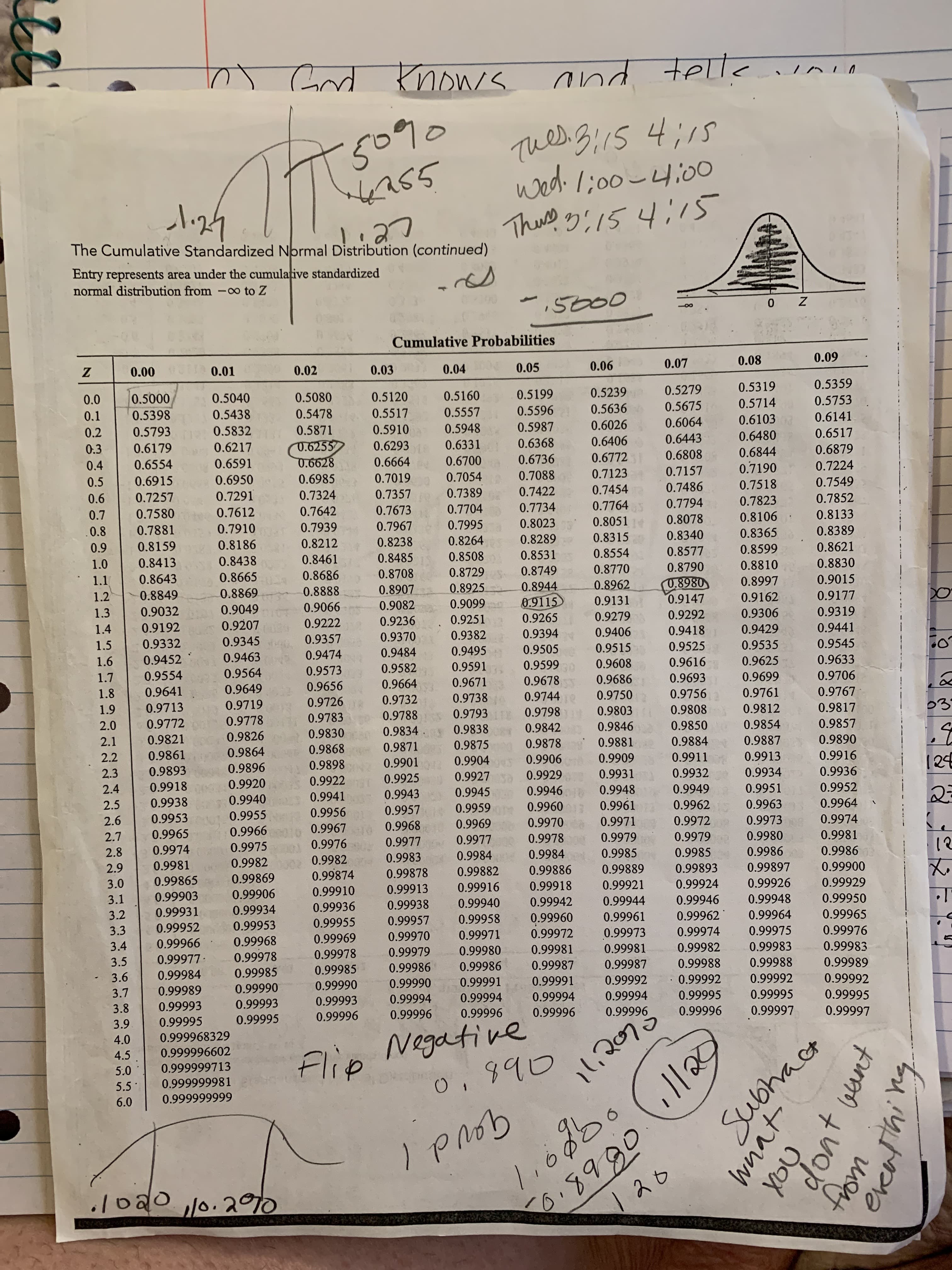
Transcribed Image Text:Cod Knows nnd telt
ALA
Tuergi15 4;15
wed 1;00-40O
Thu 154S
ass
The Cumulative Standardized Normal Distribution (continued)
Entry represents area under the cumulative standardized
normal distribution from -0o to Z
0 Z
Cumulative Probabilities
Z
0.00
0.01
0.02
0.09
0.03
0.08
0.04
0.05
0.06
0.07
0.5000
0.0
0.5040
0.5080
0.5359
0.5319
0.5120
0.5160
0.5279
0.5199
0.5239
0.1
0.5398
0.5438
0.5478
0.5753
0.5714
0.5517
0.5675
0.5557
0.5596
0.5636
0.2
0.5793
0.5832
0.6141
0.5871
0.6103
0.6064
0.5910
0.5948
0.5987
0.6026
0.3
0.6179
0.6217
0.6255
0.6628
0.6517
0.6480
0.6293
0.6443
0.6406
0.6331
0.6368
0.4
0.6554
0.6591
0.6879
0.6844
0.6664
0.6808
0.6700
0.6772
0.6736
0.6915
0.5
0.6950
0.7190
0.6985
0.7224
0.7019
0.7054
0.7157
0.7088
0.7123
0.6
0.7257
0.7291
0.7324
0.7549
0.7357
0.7389
0.7518
0.7486
0.7422
0.7454
0.7
0.7580
0.7612
0.7852
0.7642
0.7823
0.7673
0.7704
0.7734
0.7764
0.7794
.0.8
0.7881
0.7910
0.7939
0.8133
0.8106
0.7967
0.7995
0.8023
0.8051
0.8078
0.9
0.8159
0.8186
0.8212
0.8389
0.8238
0.8264
0.8365
0.8340
0.8289
0.8315
1.0
0.8413
0.8438
0.8461
0.8621
0.8508
0.8599
0.8485
0.8554
0.8577
0.8531
0.8665
1.1
0.8643
0.8686
0.8729
0.8708
0.8749
0.8790
0.8810
0.8830
0.8770
0.8925
0.8869
1.2
0.8849
0.8888
0.8907
0.8962
O.8980
0.9147
0.8997
0.8944
0.9015
0.9115
1.3
0.9066
0.9032
0.9049
0.9082
0.9099
0.9162
0.9131
0.9177
0.9207
1.4
0.9222
0.9236
0.9251
0.9192
0.9265
0.9279
0.9292
0.9306
0.9319
0.9382
0.9370
0.9394
0.9345
0.9357
0.9406
1.5
0.9332
0.9418
0.9429
0.9441
0.9484
0.9495
0.9463
0.9474
0.9505
0.9515
0.9525
1.6
0.9452
0.9535
0.9545
0.9591
0.9582
0.9599
0.9573
0.9616
0.9564
0.9608
0.9625
1.7
0.9554
0.9633
0.9664
0.9678
0.9671
0.9656
0.9686
0.9693
0.9641
0.9649
0.9699
1.8
0.9706
0.9732
0.9726
0.9738
0.9744
0.9750
0.9719
0.9756
0.9761
0.9713
1.9
0.9767
0.9798
0.9788
o3
0.9793
0.9803
0.9783
0.9808
0.9778
0.9812
0.9772
2.0
0.9817
0.9830
0.9834
0.9838
0.9842
0.9846
0.9826
0.9850
0.9854
0.9821
2.1
0.9857
0.9871
0.9875
0.9878
0.9881
0.9868
0.9864
0.9884
0.9887
0.9861
2.2
0.9890
0.9904
0.9906
0.9898
0.9901
0.9909
0.9896
0.9911
0.9893
0.9913
2.3
0.9916
0.9927
0.9929
0.9922
0.9925
0.9931
0.9932
0.9920
0.9918
0.9934
0.9936
2.4
0.9941
0.9945
0.9946
0.9943
0.9948
0.9949
0.9940
0.9938
0.9951
0.9952
2.5
0.9961
0.9960
0.9959
0.9956
0.9957
0.9962
0.9955
0.9953
0.9963
2.6
0.9964
0.9969
0.9970
0.9968
0.9967
0.9971
0.9972
0.9966
0.9965
0.9973
2.7
0.9974
0.9977
0.9977
0.9978
0.9976
0.9979
0.9975
0.9979
0.9974
0.9980
2.8
0.9981
0.9984
0.9983
0.9984
0.9982
0.9985
0.9982
0.9985
0.9981
0.9986
2.9
0.9986
0.99874
0.99878
0.99882
0.99886
0.99889
0.99869
0.99865
0.99893
0.99897
0.99900
3.0
0.99916
0.99910
0.99913
0.99918
0.99906
0.99921
0.99903
0.99924
0.99926
3.1
0.99929
0.99938
0.99936
0.99940
0.99942
0.99944
0.99934
0.99931
0.99946
0.99948
3.2
0.99950
0.99955
0.99960
0.99972
0.99957
0.99958
0.99961
0.99952
0.99953
0.99962
3.3
0.99964
0.99965
0.99970
0.99969
0.99971
0.99968
0.99966
0.99973
0.99981
0.99974
3.4
0.99975
0.99976
0.99979
0.99978
0.99980
0.99981
0.99978
0.99977
0.99982
3.5
0.99983
0.99983
0.99986
0.99985
0.99986
0.99987
0.99985
0.99987
0.99984
0.99988
3.6
0.99988
0.99989
0.99990
0.99991
0.99990
0.99991
0.99989
0.99990
0.99992
3.7
0.99992
0.99992
0.99992
0.99993
0.99994
0.99994
0.99994
0.99993
0.99993
0.99994
3.8
0.99995
0.99995
0.99995
0.99996
0.99996
0.99996
0.99995
0.99995
0.99996
0.99996
3.9
0.99996
0.99997
0.99997
0.999968329
4.0
Nagative
.l
Subhacr
0.999996602
4.5
Flip
0.999999713
5.0
0.999999981
0, 990
5.5
0.999999999
6.0
./0a0 0.2
990
dont pant
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 3 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, probability and related others by exploring similar questions and additional content below.Recommended textbooks for you

A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON


A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON
