/5. D is the midpoint of side BC of triangle ABC and the bisectors of angles ADB and ADC meet AB and AC at E and F respectively. Prove: EF is parallel to BC. (See Theo- rem 54.) AutoSave Exercises 4_15 proofs 1 and. . Marc Skwarczynski ON Exercise 4.15 #3: A triangle ABC is inscribed in a circle. M is the midpoint of AMČ and BM intersects AC at D. File Home Insert Draw Design Layout References Mailings Review View Help Table Design Layout 1D Exercises 4.15 #3 Given: Inscribed AABC; M midpoint of AMC; BM intersects AC in D AB AD Prove: %3D BC DC AB Prove: BC AD Statements Reasons DC 1. (see above) 1. Given 2. CM = AM 2. Def. of midpoint 3. ZCBM = - CM; 3. An inscribed angle = ½ the intercepted arc. %3D %3D ZABM = AM M. 4. - CM = - AM 4. Division (of step 2) %3D 2. 5. Substitution 5. ZCBM = LABM %3D (step 3 -> step 4) 6. Def. of bisector 6. BM bisects ZABC 7. The bisector of an interior angle of a divides the oppos internally into se which have the sa AB 7. BC AD %3D DC as the other two 257 words fecus
/5. D is the midpoint of side BC of triangle ABC and the bisectors of angles ADB and ADC meet AB and AC at E and F respectively. Prove: EF is parallel to BC. (See Theo- rem 54.) AutoSave Exercises 4_15 proofs 1 and. . Marc Skwarczynski ON Exercise 4.15 #3: A triangle ABC is inscribed in a circle. M is the midpoint of AMČ and BM intersects AC at D. File Home Insert Draw Design Layout References Mailings Review View Help Table Design Layout 1D Exercises 4.15 #3 Given: Inscribed AABC; M midpoint of AMC; BM intersects AC in D AB AD Prove: %3D BC DC AB Prove: BC AD Statements Reasons DC 1. (see above) 1. Given 2. CM = AM 2. Def. of midpoint 3. ZCBM = - CM; 3. An inscribed angle = ½ the intercepted arc. %3D %3D ZABM = AM M. 4. - CM = - AM 4. Division (of step 2) %3D 2. 5. Substitution 5. ZCBM = LABM %3D (step 3 -> step 4) 6. Def. of bisector 6. BM bisects ZABC 7. The bisector of an interior angle of a divides the oppos internally into se which have the sa AB 7. BC AD %3D DC as the other two 257 words fecus
Elementary Geometry For College Students, 7e
7th Edition
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Alexander, Daniel C.; Koeberlein, Geralyn M.
Chapter8: Areas Of Polygons And Circles
Section8.5: More Area Relationships In The Circle
Problem 9E
Related questions
Topic Video
Question
Theorem 54=If a line divides two sides of a
Please answer in a two-column proof-statements and reasons. **Also, it should have ONLY one given (statement).** I have an example of how it should look like/how it should be done in the second picture.
It is about lines proportional. The question is in the picture. *The question is completely clear, so please don't reject the question.*

Transcribed Image Text:/5. D is the midpoint of side BC of triangle
ABC and the bisectors of angles ADB
and ADC meet AB and AC at E and F
respectively.
Prove: EF is parallel to BC. (See Theo-
rem 54.)
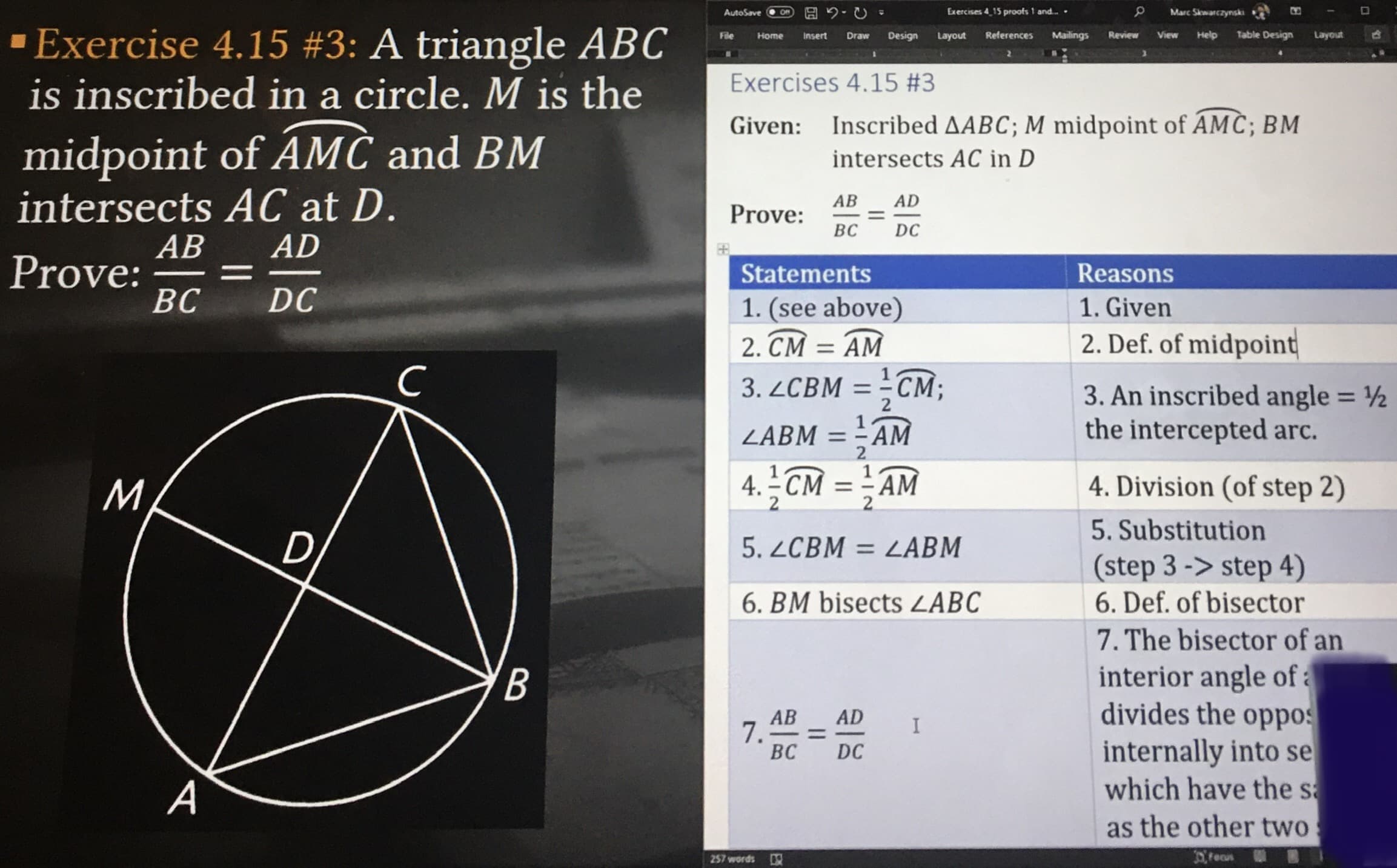
Transcribed Image Text:AutoSave
Exercises 4_15 proofs 1 and. .
Marc Skwarczynski
ON
Exercise 4.15 #3: A triangle ABC
is inscribed in a circle. M is the
midpoint of AMČ and BM
intersects AC at D.
File
Home
Insert
Draw
Design
Layout
References
Mailings
Review
View
Help
Table Design
Layout
1D
Exercises 4.15 #3
Given: Inscribed AABC; M midpoint of AMC; BM
intersects AC in D
AB AD
Prove:
%3D
BC
DC
AB
Prove:
BC
AD
Statements
Reasons
DC
1. (see above)
1. Given
2. CM = AM
2. Def. of midpoint
3. ZCBM = - CM;
3. An inscribed angle = ½
the intercepted arc.
%3D
%3D
ZABM =
AM
M.
4. - CM = - AM
4. Division (of step 2)
%3D
2.
5. Substitution
5. ZCBM = LABM
%3D
(step 3 -> step 4)
6. Def. of bisector
6. BM bisects ZABC
7. The bisector of an
interior angle of a
divides the oppos
internally into se
which have the sa
AB
7.
BC
AD
%3D
DC
as the other two
257 words
fecus
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Recommended textbooks for you

Elementary Geometry For College Students, 7e
Geometry
ISBN:
9781337614085
Author:
Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:
Cengage,

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Holt Mcdougal Larson Pre-algebra: Student Edition…
Algebra
ISBN:
9780547587776
Author:
HOLT MCDOUGAL
Publisher:
HOLT MCDOUGAL

Elementary Geometry For College Students, 7e
Geometry
ISBN:
9781337614085
Author:
Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:
Cengage,

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Holt Mcdougal Larson Pre-algebra: Student Edition…
Algebra
ISBN:
9780547587776
Author:
HOLT MCDOUGAL
Publisher:
HOLT MCDOUGAL

Elementary Geometry for College Students
Geometry
ISBN:
9781285195698
Author:
Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:
Cengage Learning

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:
9781305071742
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning

Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:
9781305658004
Author:
Ron Larson
Publisher:
Cengage Learning