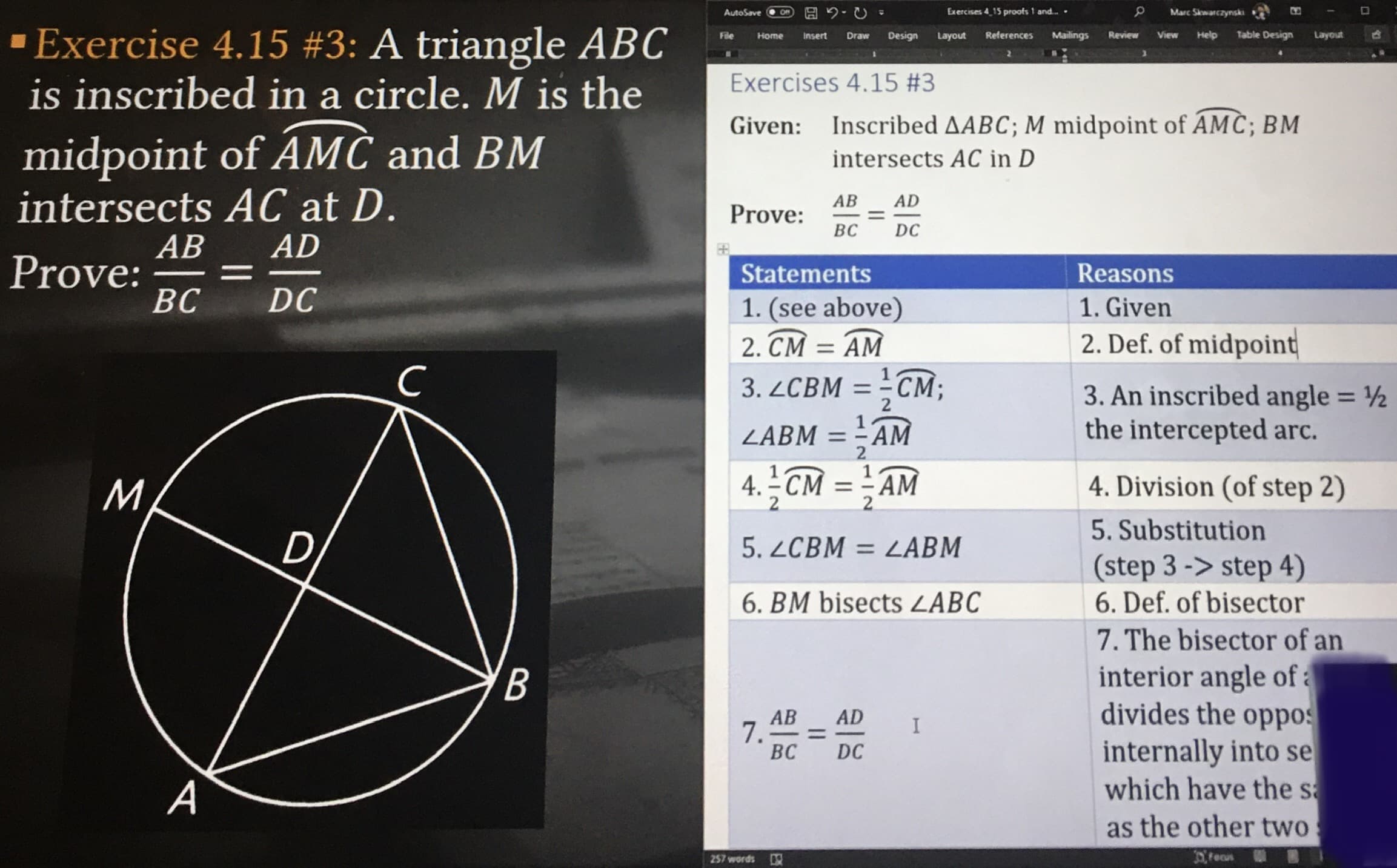
5. Given: D is the midpoint of BC of triangle ABC Prove: EF//BC Statements Reasons 1.D is the midpoint of side BC of triangle 1.Given ABC and the bisectors of angles ADB and ADC meet AB and AC at E and F respectively 3.Triangle ABC = triangle AEF 3.lf two angles of one triangle are equal respectively to two angles of another, then the triangle are similar. (a.a.) 4.AE + EB = AB & AF+FC = AC 4.Segment Addition Postulate %3D 5.Triangle BDE = triangle ADE & triangle CDF = triangle ADF 5.Definition of angle bisector %3D 6.Corresponding sides of similar triangles are proportional (C.S.S.T.P.) 6.AE/EB = AF/FC %3D 7.Angle ABD = angle AEF & angle BCA = 7.Corresponding Angles Postulate angle EFA %3D 8.DE bisects AB and DF bisects AC 8. proportionally 9. If a line divides two sides of a triangle proportionally, then it is parallel to the third side. (Theorem 54) 9.EF // BC ET !! AutoSave Exercises 4_15 proofs 1 and. . Marc Skwarczynski ON Exercise 4.15 #3: A triangle ABC is inscribed in a circle. M is the midpoint of AMČ and BM intersects AC at D. File Home Insert Draw Design Layout References Mailings Review View Help Table Design Layout 1D Exercises 4.15 #3 Given: Inscribed AABC; M midpoint of AMC; BM intersects AC in D AB AD Prove: %3D BC DC AB Prove: BC AD Statements Reasons DC 1. (see above) 1. Given 2. CM = AM 2. Def. of midpoint 3. ZCBM = - CM; 3. An inscribed angle = ½ the intercepted arc. %3D %3D ZABM = AM M. 4. - CM = - AM 4. Division (of step 2) %3D 2. 5. Substitution 5. ZCBM = LABM %3D (step 3 -> step 4) 6. Def. of bisector 6. BM bisects ZABC 7. The bisector of an interior angle of a divides the oppos internally into se which have the sa AB 7. BC AD %3D DC as the other two 257 words fecus
Please help with this two-column proof. Just fill in the statements and reasons in the missing blanks. *There is an example of how it looks like when it is done in the second picture.*
The proof is in the picture. **This is about proving the triangle true, not about writing essay.**
*Maybe, if you think those reasons below suit the statements, you can use it.* (Those below are the reasons you can use to prove the statements true if you think it is suited for it.)
Definition of ~
Definition of bisector
Definition of perimeter
Definition of median
Definition of midpoint
Multiplication
Division
An inscribed angle = 1/2 the intercepted arc
If 4 quantities are in proportion, then like powers are in proportion.
Subtraction Transformation
Alternation Transformation
Pythagorean Theorem
If 2
In a series of equal ratios, the sum of the antecedents is to the sum of the consequents as any antecedent is to its consequent.
In any proportion the product of the means equals the product of the extremes.
Angles inscribed in the same segment or equal segments are equal.
If a line is drawn parallel to the base of a triangle, it cuts off a triangle similar to the given triangle.
Two isosceles triangles are similar if any angle of one equals the corresponding angle of the other.

Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 4 images






