8. For the quadratic functions a. f(x) = -3z2 6x - 1, b. g(x) = 2x1 (a) Find the vertex form. What is the vertex? (b) Find the x and y intercepts of the above function. (c) Find the domain and the range (d) Find the maximum or the minimum. (e) Write a brief verbal description of the relationship between the graph of the above quadratic and the graph of h(x) x2.
8. For the quadratic functions a. f(x) = -3z2 6x - 1, b. g(x) = 2x1 (a) Find the vertex form. What is the vertex? (b) Find the x and y intercepts of the above function. (c) Find the domain and the range (d) Find the maximum or the minimum. (e) Write a brief verbal description of the relationship between the graph of the above quadratic and the graph of h(x) x2.
College Algebra
7th Edition
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:James Stewart, Lothar Redlin, Saleem Watson
Chapter3: Polynomial And Rational Functions
Section3.1: Quadratic Functions And Models
Problem 1E: To put the quadratic function f(x)=ax2+bx+c in standard form, we complete the ________________.
Related questions
Question
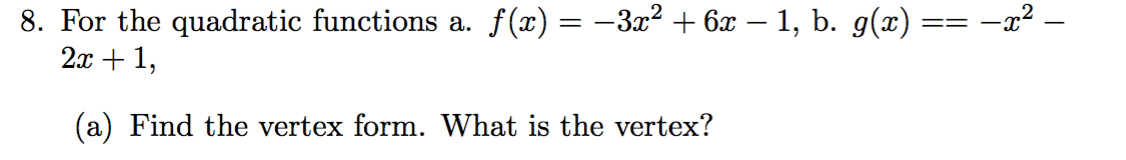
Transcribed Image Text:8. For the quadratic functions a. f(x) = -3z2 6x - 1, b. g(x) =
2x1
(a) Find the vertex form. What is the vertex?

Transcribed Image Text:(b) Find the x and y intercepts of the above function.
(c) Find the domain and the range
(d) Find the maximum or the minimum.
(e) Write a brief verbal description of the relationship between the graph
of the above quadratic and the graph of h(x) x2.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 6 steps with 6 images

Recommended textbooks for you

College Algebra
Algebra
ISBN:
9781305115545
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage


College Algebra
Algebra
ISBN:
9781305115545
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage


Algebra: Structure And Method, Book 1
Algebra
ISBN:
9780395977224
Author:
Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:
McDougal Littell

Algebra for College Students
Algebra
ISBN:
9781285195780
Author:
Jerome E. Kaufmann, Karen L. Schwitters
Publisher:
Cengage Learning

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:
9781305071742
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning