9 Graph the function y = 2x2 x-1 2-1 by identifying the domain and any symmetries, finding the derivatives y and y", finding the critical points and identifying the function's behavior at each one, finding where the curve is increasing and where it is decreasing, finding the points of inflection, determining the concavity of the curve, identifying any asymptotes, and plotting any key points such as intercepts, critical points, and inflection points. Then find coordinates of absolute extreme points, if any. Find the domain of the function The domain is (Type your answer in interval notation.) Identify any symmetries. Choose the correct answer below. O A. The function is an even function that is symmetric about the origin. O B. The function is an even function that is symmetric about the y-axis. O C. The function is not symmetric. O D. The function is an odd function that is symmetric about the origin O E. The function is an odd function that is symmetric about the y-axis. Find the derivative y' у 3 Find the second derivative y". у3 Identify any critical points. Select the correct choice below and, if necessary, fill in the answer box to complete your choice O A. The critical point(s) occur(s) at x= (Use a comma to separate answers as needed.) O B. There are no critical points. Identify any local minima. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. The local minimum/minima is/are located at (Type an ordered pair. Use a comma to separate answers as needed.) O B. There are no local minima. Identify any local maxima. Select the correct choice below and, if necessary, fill in the answer box to complete your choice O A. The local maximum/maxima is/are located at (Type an ordered pair. Use a comma to separate answers as needed.) O B. There are no local maxima. Identify where the curve is increasing or decreasing. Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice. O A. The curve increases on the open interval(s) and does not decrease. (Type your answer in interval notation. Use a comma to separate answers as needed.) O B. The curve does not increase and decreases on the open interval(s) (Type your answer in interval notation. Use a comma to separate answers as needed.) O C. The curve increases on the open interval(s) and decreases on the open interval(s) (Type your answers in interval notation. Use a comma to separate answers as needed.) O D. The curve neither increases nor decreases. Identify any inflection points. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. The inflection point(s) is/are (Type an ordered pair. Use a comma to separate answers as needed.) O B. There are no inflection points. Identify where the curve is concave up or concave down. Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice. O A. The curve is concave up on the interval(s) and is concave down on the interval(s) (Type your answers in interval notation. Use a comma to separate answers as needed.) O B. The curve is never concave up and is concave down on the interval(s) (Type your answer in interval notation. Use a comma to separate answers as needed.) O C. The curve is concave up on the interval(s) and is never concave down. (Type your answer in interval notation. Use a comma to separate answers as needed.) O D. The curve is neither concave up nor concave down. Find any vertical asymptotes. Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice. O A. The function has one vertical asymptote, (Type an equation.) O B. The function has two vertical asymptotes. The leftmost asymptote is and the rightmost asymptote is (Type equations.) O C. The function has no vertical asymptotes. Find any horizontal asymptotes. Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice. O A. The function has one horizontal asymptote, (Type an equation.) O B. The function has two horizontal asymptotes. The top asymptote is and the bottom asymptote is (Type equations.) O C. The function has no horizontal asymptotes Find any oblique asymptotes. Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice. O A. The function has one oblique asymptote, (Type an equation.) O B. The function has two oblique asymptotes. The asymptote with smaller slope is and the asymptote with larger slope is (Type equations.) O C. The function has no oblique asymptotes 2x2x1 x2 -1 Graph the function y Choose the correct graph below. O C. O A. ОВ. OD. Ay Identify the absolute maximum value and where it occurs. Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice O A. The absolute maximum value occurs at X (Use a comma to separate answers as needed. Type each answer only once.) O B. There is no absolute maximum Identify the absolute minimum value and where it occurs. Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice. O A. The absolute minimum value OCcurs at x = (Use a comma to separate answers as needed. Type each answer only once.) O B. There is no absolute minimum.
9 Graph the function y = 2x2 x-1 2-1 by identifying the domain and any symmetries, finding the derivatives y and y", finding the critical points and identifying the function's behavior at each one, finding where the curve is increasing and where it is decreasing, finding the points of inflection, determining the concavity of the curve, identifying any asymptotes, and plotting any key points such as intercepts, critical points, and inflection points. Then find coordinates of absolute extreme points, if any. Find the domain of the function The domain is (Type your answer in interval notation.) Identify any symmetries. Choose the correct answer below. O A. The function is an even function that is symmetric about the origin. O B. The function is an even function that is symmetric about the y-axis. O C. The function is not symmetric. O D. The function is an odd function that is symmetric about the origin O E. The function is an odd function that is symmetric about the y-axis. Find the derivative y' у 3 Find the second derivative y". у3 Identify any critical points. Select the correct choice below and, if necessary, fill in the answer box to complete your choice O A. The critical point(s) occur(s) at x= (Use a comma to separate answers as needed.) O B. There are no critical points. Identify any local minima. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. The local minimum/minima is/are located at (Type an ordered pair. Use a comma to separate answers as needed.) O B. There are no local minima. Identify any local maxima. Select the correct choice below and, if necessary, fill in the answer box to complete your choice O A. The local maximum/maxima is/are located at (Type an ordered pair. Use a comma to separate answers as needed.) O B. There are no local maxima. Identify where the curve is increasing or decreasing. Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice. O A. The curve increases on the open interval(s) and does not decrease. (Type your answer in interval notation. Use a comma to separate answers as needed.) O B. The curve does not increase and decreases on the open interval(s) (Type your answer in interval notation. Use a comma to separate answers as needed.) O C. The curve increases on the open interval(s) and decreases on the open interval(s) (Type your answers in interval notation. Use a comma to separate answers as needed.) O D. The curve neither increases nor decreases. Identify any inflection points. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. The inflection point(s) is/are (Type an ordered pair. Use a comma to separate answers as needed.) O B. There are no inflection points. Identify where the curve is concave up or concave down. Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice. O A. The curve is concave up on the interval(s) and is concave down on the interval(s) (Type your answers in interval notation. Use a comma to separate answers as needed.) O B. The curve is never concave up and is concave down on the interval(s) (Type your answer in interval notation. Use a comma to separate answers as needed.) O C. The curve is concave up on the interval(s) and is never concave down. (Type your answer in interval notation. Use a comma to separate answers as needed.) O D. The curve is neither concave up nor concave down. Find any vertical asymptotes. Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice. O A. The function has one vertical asymptote, (Type an equation.) O B. The function has two vertical asymptotes. The leftmost asymptote is and the rightmost asymptote is (Type equations.) O C. The function has no vertical asymptotes. Find any horizontal asymptotes. Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice. O A. The function has one horizontal asymptote, (Type an equation.) O B. The function has two horizontal asymptotes. The top asymptote is and the bottom asymptote is (Type equations.) O C. The function has no horizontal asymptotes Find any oblique asymptotes. Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice. O A. The function has one oblique asymptote, (Type an equation.) O B. The function has two oblique asymptotes. The asymptote with smaller slope is and the asymptote with larger slope is (Type equations.) O C. The function has no oblique asymptotes 2x2x1 x2 -1 Graph the function y Choose the correct graph below. O C. O A. ОВ. OD. Ay Identify the absolute maximum value and where it occurs. Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice O A. The absolute maximum value occurs at X (Use a comma to separate answers as needed. Type each answer only once.) O B. There is no absolute maximum Identify the absolute minimum value and where it occurs. Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice. O A. The absolute minimum value OCcurs at x = (Use a comma to separate answers as needed. Type each answer only once.) O B. There is no absolute minimum.
Functions and Change: A Modeling Approach to College Algebra (MindTap Course List)
6th Edition
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Bruce Crauder, Benny Evans, Alan Noell
Chapter5: A Survey Of Other Common Functions
Section5.6: Higher-degree Polynomials And Rational Functions
Problem 14E
Related questions
Topic Video
Question
Can you help with this problem step by step?
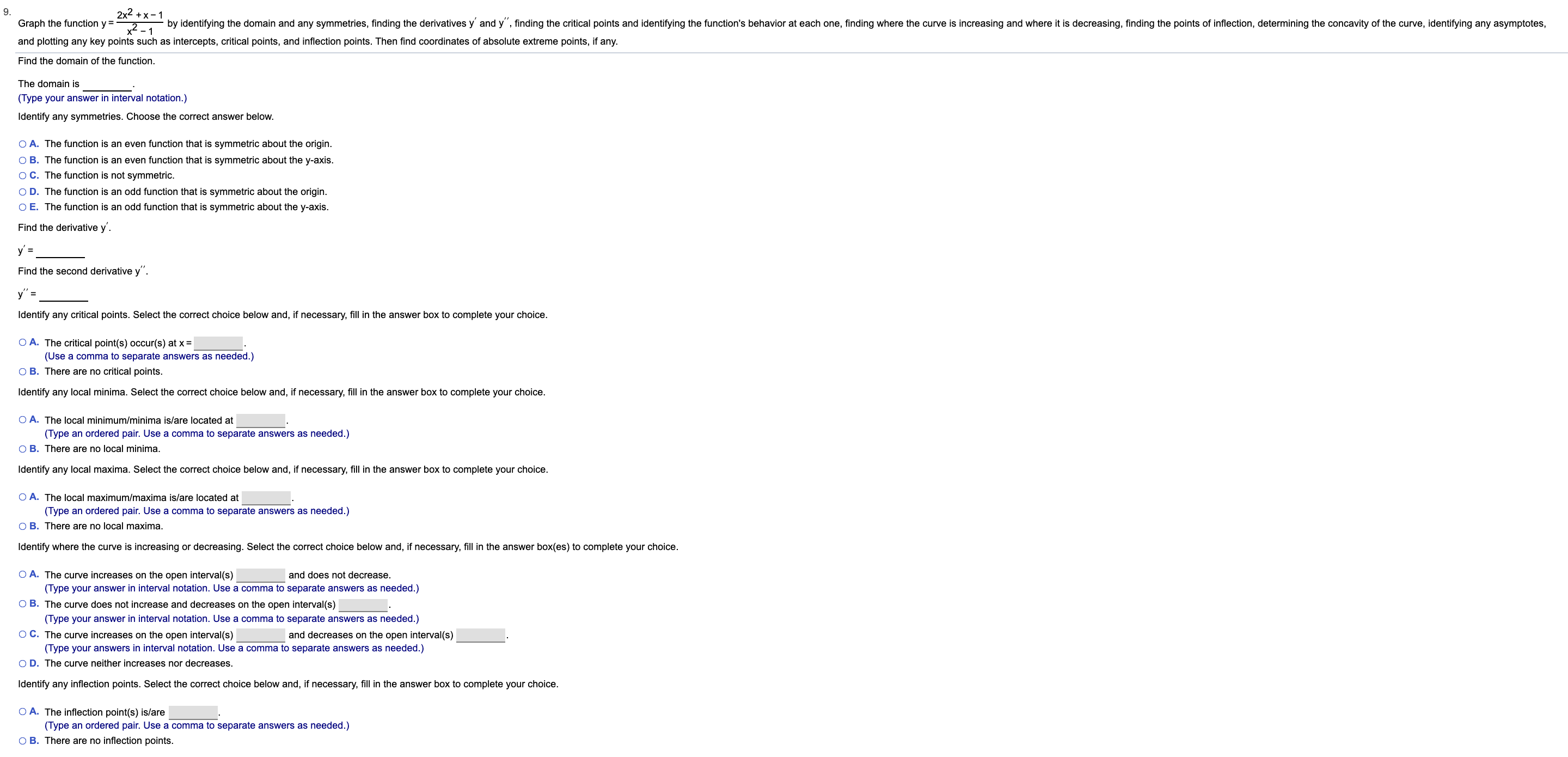
Transcribed Image Text:9
Graph the function y =
2x2 x-1
2-1
by identifying the domain and any symmetries, finding the derivatives y and y", finding the critical points and identifying the function's behavior at each one, finding where the curve is increasing and where it is decreasing, finding the points of inflection, determining the concavity of the curve, identifying any asymptotes,
and plotting any key points such as intercepts, critical points, and inflection points. Then find coordinates of absolute extreme points, if any.
Find the domain of the function
The domain is
(Type your answer in interval notation.)
Identify any symmetries. Choose the correct answer below.
O A. The function is an even function that is symmetric about the origin.
O B. The function is an even function that is symmetric about the y-axis.
O C. The function is not symmetric.
O D. The function is an odd function that is symmetric about the origin
O E. The function is an odd function that is symmetric about the y-axis.
Find the derivative y'
у 3
Find the second derivative y".
у3
Identify any critical points. Select the correct choice below and, if necessary, fill in the answer box to complete your choice
O A. The critical point(s) occur(s) at x=
(Use a comma to separate answers as needed.)
O B. There are no critical points.
Identify any local minima. Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
O A. The local minimum/minima is/are located at
(Type an ordered pair. Use a comma to separate answers as needed.)
O B. There are no local minima.
Identify any local maxima. Select the correct choice below and, if necessary, fill in the answer box to complete your choice
O A. The local maximum/maxima is/are located at
(Type an ordered pair. Use a comma to separate answers as needed.)
O B. There are no local maxima.
Identify where the curve is increasing or decreasing. Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice.
O A. The curve increases on the open interval(s)
and does not decrease.
(Type your answer in interval notation. Use a comma to separate answers as needed.)
O B. The curve does not increase and decreases on the open interval(s)
(Type your answer in interval notation. Use a comma to separate answers as needed.)
O C. The curve increases on the open interval(s)
and decreases on the open interval(s)
(Type your answers in interval notation. Use a comma to separate answers as needed.)
O D. The curve neither increases nor decreases.
Identify any inflection points. Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
O A. The inflection point(s) is/are
(Type an ordered pair. Use a comma to separate answers as needed.)
O B. There are no inflection points.

Transcribed Image Text:Identify where the curve is concave up or concave down. Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice.
O A. The curve is concave up on the interval(s)
and is concave down on the interval(s)
(Type your answers in interval notation. Use a comma to separate answers as needed.)
O B. The curve is never concave up and is concave down on the interval(s)
(Type your answer in interval notation. Use a comma to separate answers as needed.)
O C. The curve is concave up on the interval(s)
and is never concave down.
(Type your answer in interval notation. Use a comma to separate answers as needed.)
O D. The curve is neither concave up nor concave down.
Find any vertical asymptotes. Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice.
O A. The function has one vertical asymptote,
(Type an equation.)
O B. The function has two vertical asymptotes. The leftmost asymptote is
and the rightmost asymptote is
(Type equations.)
O C. The function has no vertical asymptotes.
Find any horizontal asymptotes. Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice.
O A. The function has one horizontal asymptote,
(Type an equation.)
O B. The function has two horizontal asymptotes. The top asymptote is
and the bottom asymptote is
(Type equations.)
O C. The function has no horizontal asymptotes
Find any oblique asymptotes. Select the correct choice below and, if necessary, fill in the answer box(es) to complete your choice.
O A. The function has one oblique asymptote,
(Type an equation.)
O B. The function has two oblique asymptotes. The asymptote with smaller slope is
and the asymptote with larger slope is
(Type equations.)
O C. The function has no oblique asymptotes
2x2x1
x2 -1
Graph the function y
Choose the correct graph below.
O C.
O A.
ОВ.
OD.
Ay
Identify the absolute maximum value and where it occurs. Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice
O A. The absolute maximum value
occurs at X
(Use a comma to separate answers as needed. Type each answer only once.)
O B. There is no absolute maximum
Identify the absolute minimum value and where it occurs. Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
O A. The absolute minimum value
OCcurs at x =
(Use a comma to separate answers as needed. Type each answer only once.)
O B. There is no absolute minimum.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 6 steps with 6 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Recommended textbooks for you

Functions and Change: A Modeling Approach to Coll…
Algebra
ISBN:
9781337111348
Author:
Bruce Crauder, Benny Evans, Alan Noell
Publisher:
Cengage Learning

College Algebra (MindTap Course List)
Algebra
ISBN:
9781305652231
Author:
R. David Gustafson, Jeff Hughes
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Functions and Change: A Modeling Approach to Coll…
Algebra
ISBN:
9781337111348
Author:
Bruce Crauder, Benny Evans, Alan Noell
Publisher:
Cengage Learning

College Algebra (MindTap Course List)
Algebra
ISBN:
9781305652231
Author:
R. David Gustafson, Jeff Hughes
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage
