Rotational Equilibrium And Rotational Dynamics
In physics, the state of balance between the forces and the dynamics of motion is called the equilibrium state. The balance between various forces acting on a system in a rotational motion is called rotational equilibrium or rotational dynamics.
Equilibrium of Forces
The tension created on one body during push or pull is known as force.
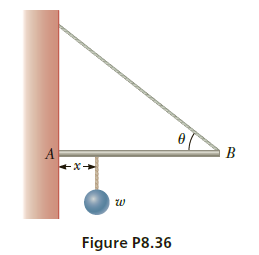
One end of a uniform
4.0-m-long rod of weight
w is supported by a cable
at an angle of θ = 37° with
the rod. The other end
rests against a wall, where it
is held by friction. (See Fig.
P8.36.) The coefficient of
static friction between the
wall and the rod is μs = 0.50.
Determine the minimum
distance x from point A at
which an additional weight w (the same as the weight of the
rod) can be hung without causing the rod to slip at point A.
Trending now
This is a popular solution!
Step by step
Solved in 5 steps with 4 images








