A golf ball manufacturer knows the cost associated with various hourly production levels, given below. Production Costs for Golf Balls Production (hundred balls b) Cost (dollars C) 247 354 431 11 497 14 531 17 565 20 623 (a) Write a cubic model for the data. (Round all numerical values to three decimal places.) C(b) = 0.0669b3 – 2.899962 + 54.953b + 146.35 dollars is the production cost when the hourly production rate is b hundred golf balls 2 sbs 20. (b) If 1000 balls are currently being produced each hour, calculate the marginal cost at that level of production. (Round your answer to two decimal places.) $ 17.25 X per hundred balls Interpret the result. (Round your numerical answer to two decimal places.) At an hourly production level of 1000 golf balls, production cost is increasing by $ 17.225 X per hundred golf balls.
A golf ball manufacturer knows the cost associated with various hourly production levels, given below. Production Costs for Golf Balls Production (hundred balls b) Cost (dollars C) 247 354 431 11 497 14 531 17 565 20 623 (a) Write a cubic model for the data. (Round all numerical values to three decimal places.) C(b) = 0.0669b3 – 2.899962 + 54.953b + 146.35 dollars is the production cost when the hourly production rate is b hundred golf balls 2 sbs 20. (b) If 1000 balls are currently being produced each hour, calculate the marginal cost at that level of production. (Round your answer to two decimal places.) $ 17.25 X per hundred balls Interpret the result. (Round your numerical answer to two decimal places.) At an hourly production level of 1000 golf balls, production cost is increasing by $ 17.225 X per hundred golf balls.
Functions and Change: A Modeling Approach to College Algebra (MindTap Course List)
6th Edition
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Bruce Crauder, Benny Evans, Alan Noell
Chapter5: A Survey Of Other Common Functions
Section5.5: Quadratic Functions
Problem 3TU: TEST FOR UNDERSTANDING FOR EXAMPLE 5.16 In the study Economics of Scale in High School Operation by...
Related questions
Question
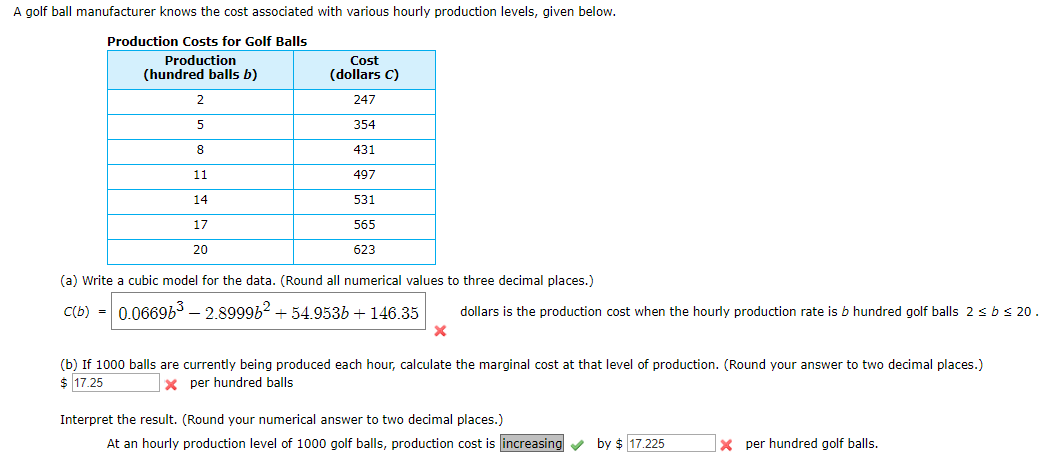
Transcribed Image Text:A golf ball manufacturer knows the cost associated with various hourly production levels, given below.
Production Costs for Golf Balls
Production
(hundred balls b)
Cost
(dollars C)
247
354
431
11
497
14
531
17
565
20
623
(a) Write a cubic model for the data. (Round all numerical values to three decimal places.)
C(b) = 0.0669b3 – 2.899962 + 54.953b + 146.35
dollars is the production cost when the hourly production rate is b hundred golf balls 2
sbs 20.
(b) If 1000 balls are currently being produced each hour, calculate the marginal cost at that level of production. (Round your answer to two decimal places.)
$ 17.25
X per hundred balls
Interpret the result. (Round your numerical answer to two decimal places.)
At an hourly production level of 1000 golf balls, production cost is increasing
by $ 17.225
X per hundred golf balls.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 4 images

Recommended textbooks for you

Functions and Change: A Modeling Approach to Coll…
Algebra
ISBN:
9781337111348
Author:
Bruce Crauder, Benny Evans, Alan Noell
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Functions and Change: A Modeling Approach to Coll…
Algebra
ISBN:
9781337111348
Author:
Bruce Crauder, Benny Evans, Alan Noell
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Glencoe Algebra 1, Student Edition, 9780079039897…
Algebra
ISBN:
9780079039897
Author:
Carter
Publisher:
McGraw Hill

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning