(a) Let A and B be square matrices that are unitarily equivalent. Prove that ||A||= ||B||. (b) Let T be a linear operator on a finite-dimensional inner product space V. Define Prove that ||T||= || [T]β||, where β is any orthonormal basis for V. (c) Let V be an infinite-dimensional inner product space with an orthonormal basis {v1, v2, . . .}. Let T be the linear operator on V such that T(vk) = kvk. Prove that ||T|| (defined in (b)) does not exist.
(a) Let A and B be square matrices that are unitarily equivalent. Prove that ||A||= ||B||. (b) Let T be a linear operator on a finite-dimensional inner product space V. Define Prove that ||T||= || [T]β||, where β is any orthonormal basis for V. (c) Let V be an infinite-dimensional inner product space with an orthonormal basis {v1, v2, . . .}. Let T be the linear operator on V such that T(vk) = kvk. Prove that ||T|| (defined in (b)) does not exist.
Linear Algebra: A Modern Introduction
4th Edition
ISBN:9781285463247
Author:David Poole
Publisher:David Poole
Chapter6: Vector Spaces
Section6.6: The Matrix Of A Linear Transformation
Problem 43EQ
Related questions
Question
(a) Let A and B be square matrices that are unitarily equivalent. Prove that ||A||= ||B||.
(b) Let T be a linear operator on a finite-dimensional inner product space V. Define Prove that ||T||= || [T]β||, where β is any orthonormal basis for V.
(c) Let V be an infinite-dimensional inner product space with an orthonormal basis {v1, v2, . . .}. Let T be the linear operator on V such that T(vk) = kvk. Prove that ||T|| (defined in (b)) does not exist.
Expert Solution
Step 1
We’ll answer the first question since the exact one wasn’t specified. Please submit a new question specifying the one you’d like answered
Step 2
Given A and B is unitary equivalent square matrices.
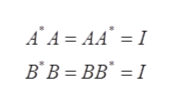
Step 3
Let
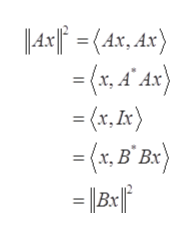
Step by step
Solved in 5 steps with 4 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Elements Of Modern Algebra
Algebra
ISBN:
9781285463230
Author:
Gilbert, Linda, Jimmie
Publisher:
Cengage Learning,

Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:
9781305658004
Author:
Ron Larson
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Elements Of Modern Algebra
Algebra
ISBN:
9781285463230
Author:
Gilbert, Linda, Jimmie
Publisher:
Cengage Learning,

Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:
9781305658004
Author:
Ron Larson
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage