Homework Help is Here – Start Your Trial Now!
Math
Statistics
A random sample of n observations is selected from a normal population to test the null hypothesis that u= 10. Specify the rejection region for each of the following combinations of H, a, and n. a. Ha 10, o= 0.05; n = 14 b. Ha > 10; a= 0.10; n = 24 C. Ha: d. Ha: 10; a= 0.10; n = 1 1 e. Ha u 10; a 0.01 ; n = 22 1. Η. με 10 , α-0.05, n-5 10, a= 0.01; n = 12 frect: 0 c. Select the correct choice below and fill in the answer box within your choice. y (Round to three decimal places as needed.) O A. It O B. t O C. t Click to select and enter your answer(s) and then click Check Answer 3 parts remaining Check Answer Clear All Tarms of Llce tion Inc All rights rase 2019 Pearson l Convriaht here to search

A random sample of n observations is selected from a normal population to test the null hypothesis that u= 10. Specify the rejection region for each of the following combinations of H, a, and n. a. Ha 10, o= 0.05; n = 14 b. Ha > 10; a= 0.10; n = 24 C. Ha: d. Ha: 10; a= 0.10; n = 1 1 e. Ha u 10; a 0.01 ; n = 22 1. Η. με 10 , α-0.05, n-5 10, a= 0.01; n = 12 frect: 0 c. Select the correct choice below and fill in the answer box within your choice. y (Round to three decimal places as needed.) O A. It O B. t O C. t Click to select and enter your answer(s) and then click Check Answer 3 parts remaining Check Answer Clear All Tarms of Llce tion Inc All rights rase 2019 Pearson l Convriaht here to search

Algebra & Trigonometry with Analytic Geometry
Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter10: Sequences, Series, And Probability
Section10.8: Probability
Problem 31E
See similar textbooks
icon
Related questions
Question
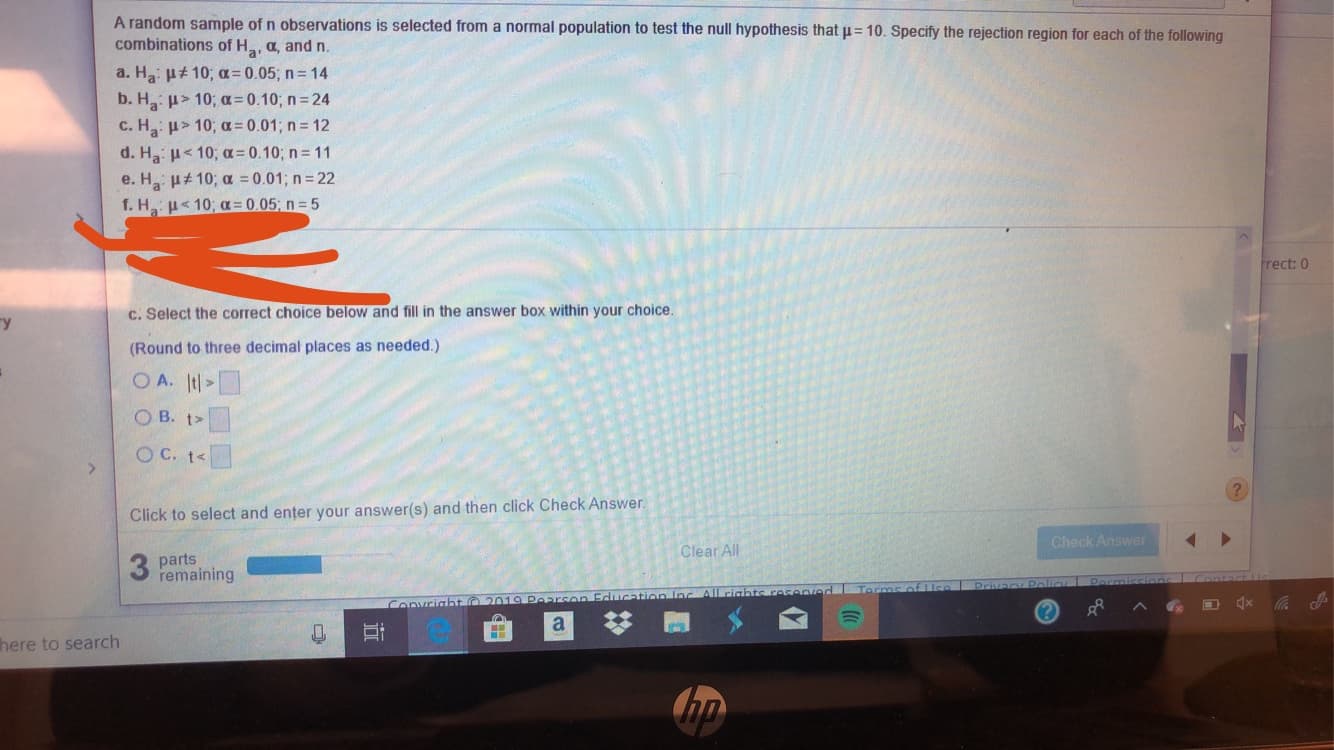
A random sample of n observations is selected from a normal population to test the null hypothesis that u= 10. Specify the rejection region for each of the following combinations of H, a, and n. a. Ha 10, o= 0.05; n = 14 b. Ha > 10; a= 0.10; n = 24 C. Ha: d. Ha: 10; a= 0.10; n = 1 1 e. Ha u 10; a 0.01 ; n = 22 1. Η. με 10 , α-0.05, n-5 10, a= 0.01; n = 12 frect: 0 c. Select the correct choice below and fill in the answer box within your choice. y (Round to three decimal places as needed.) O A. It O B. t O C. t Click to select and enter your answer(s) and then click Check Answer 3 parts remaining Check Answer Clear All Tarms of Llce tion Inc All rights rase 2019 Pearson l Convriaht here to search
Transcribed Image Text:A random sample of n observations is selected from a normal population to test the null hypothesis that u= 10. Specify the rejection region for each of the following combinations of H, a, and n. a. Ha 10, o= 0.05; n = 14 b. Ha > 10; a= 0.10; n = 24 C. Ha: d. Ha: 10; a= 0.10; n = 1 1 e. Ha u 10; a 0.01 ; n = 22 1. Η. με 10 , α-0.05, n-5 10, a= 0.01; n = 12 frect: 0 c. Select the correct choice below and fill in the answer box within your choice. y (Round to three decimal places as needed.) O A. It O B. t O C. t Click to select and enter your answer(s) and then click Check Answer 3 parts remaining Check Answer Clear All Tarms of Llce tion Inc All rights rase 2019 Pearson l Convriaht here to search
Expert Solution
trending now

Trending now

This is a popular solution!

steps

Step by step

Solved in 4 steps with 1 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Similar questions
  • SEE MORE QUESTIONS
Recommended textbooks for you
Algebra & Trigonometry with Analytic Geometry
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage
SEE MORE TEXTBOOKS