A. 4 m L-L-LH И1 L-L L-L L-L-LFL-L-L A в, |(VA)ı (VA)2 plane of (VB)1 ф2 contact (Ув)2 Фт line of impact- X.
Oblique Impact
To analyze an oblique impact using the conservation of momentum and coefficient of restitution.
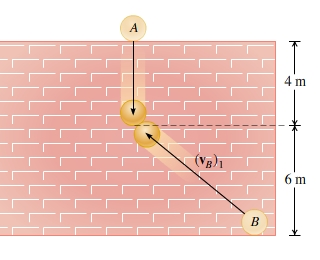
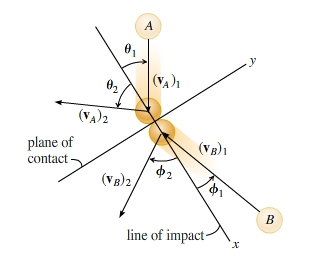
When an oblique impact occurs between two smooth particles, the particles move away from each other with velocity
∑m(vx)1=∑m(vx)2
The coefficient of restitution, e, relates the relative-velocity components of the particles along the line of impact (the x axis):
e=(vBx)2−(vAx)2(vAx)1−(vBx)1
The momenta of both particles A and B are conserved in the plane of contact (the y axis) because no impulse acts on either particle in this plane. Therefore, the y component of the velocities before and after the collisions remains unchanged:
(vy)1=(vy)2
As shown, tennis ball A rolls off the top of a 10.0 m high wall, falls 4.00 m, and strikes another tennis ball, B, obliquely. (Figure 1) Before the collision, tennis ball B has a speed of 23.0 m/s as it moves upward. Each ball's mass is 57.0 g and the collision's coefficient of restitution is 0.630. (Figure 2) In the figure, θ1=30.0∘ and ϕ1=20.0∘. What is (vA)1, the velocity of tennis ball A, immediately before the collision?
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 1 images


