Anisotropic Oscillator Consider a two-dimensional anisotropic oscillator is rational (that is, ws/wy = p/q 4. Prove that if the ratio of the frequencies w and wy where p and q are integers with gcd(p, q) = 1, where gcd stands for greatest common divisor) then the motion is periodic. Determine the period. P
Q: What is the wave-particle duality?
A: Wave-particle duality states that the light and the matter exhibit the properties of both the waves ...
Q: During your summer internship for an aerospace company, you are asked to design a small research roc...
A: Given Information :Rocket is launched from rest .Initial velocity of the rocket u = 0Maximum height ...
Q: 3.0 kg, what is the tension (in N) in the connecting string? As shown below, the coefficient of kine...
A:
Q: What is angular momentum?
A: Angular momentum:Angular momentum (l) of a particle around point A where, p is the linear momentum o...
Q: (10%) Problem 2: An electric field E(x,y,z) y(x1+y2N(x4y2) j + 2zk) passes through the square that i...
A: An electric field is given by,
Q: How do you use the Schrodinger equation to determine a particle’s position in free space?
A: The one Dimensional Time dependent Schrodinger wave equation for a particle in a potential V(x,t) is...
Q: a ball is thrown upward with an initial velocity of 20 m/ s, how long does it take before it has a v...
A: Using equation of motion, the time taken for ball to come to rest momentarily at maximum height from...
Q: In astronomy what does it mean when asked about the altitude when it comes to the moon?
A: in astronomy altitude is defined as the angular distance measured from the astronomical horizon to t...
Q: This is a problem in the field of quantum mechanics.
A: Write the given expression and multiply with both sides.
Q: what is the speed of light
A: The speed of light in vacuum is 299792458 m/s.Most commonly the speed of light in vacuum is approxim...
Q: Suppose 6.36 moles of a monatomic ideal gas expand adiabatically, and its temperature decreases from...
A: 6.36 moles of a monoatomic ideal gas expand adiabatically with decrease in temperature from 387 K to...
Q: (10%) Problem 6: A conducting spherical shell of inner radius R1 and outer radius R2 has a point cha...
A: A conducting spherical shell of inner radius R1 and outer radius R2. A point charge +q is fixed at t...
Q: A turbocharged aircraft engine cylinder has a total volume of 80 cu. in. and a clearance volume of 1...
A: Given that ,Total Volume = Volume of the cylinder before compression V1 = Vs + Vc = 80 in3Clearance ...
Q: What is a boson? Is a gluon the same thing? How do they work? What makes up electrons?
A: The following Standard model table differentiates between the Bosons and the Fermions on the basis o...
Q: In 1816, Robert Stirling, a Scottish clergyman, patented the Stirling engine, which has found a wide...
A: (a) The heat energy in an isothermal process can be written as
Q: What is a quantum system?
A: A quantum system is a portion of the whole universe which is taken under consideration to make analy...
Q: Exercise: Ball Thrown Up at the Edge of a Cliff A ball is thrown up at speed 15.0 m/s by person on t...
A: The figure shows a ball is thrown at initial velocity (voy ) along y-axis and the given coordinate s...
Q: (10%) Problem 4: A solid aluminum sphere of radius r! 0.038 m is charged with qi = +42 μC of electri...
A: Thank you for the question, since we are entitled to answer up to 3 sub-parts, we’ll answer the firs...
Q: 1
A: It is asked to proave the mean value theorem.
Q: See image question.
A: Expectation value of Sx is,
Q: If a 35.2%-efficient Carnot heat engine (left figure) is run in reverse so as to form a refrigerator...
A:
Q: (10%) Problem 8: An infinite solid insulating cylinder of radius R and has a uniform volume charge d...
A: An infinite solid insulating cylinder of radius R and has a uniform volume charge density 1.3 µC/m2....
Q: State the total number of quantum states available to an electron in the levels in a hydrogen atom t...
A: In the above problem it is assumed that the expression for the energy of an electron in a hydrogen a...
Q: What is the mass of the sun
A: Mass of the Sun can be calculated using following steps.Gravitational force of attraction between ea...
Q: Please help me with this question.
A: In natural vibrations we assume there is no friction.Since there is no friction, total energy of the...
Q: What is a black hole?
A: It is a large amount of dense matter concentrated in a small region of space with incredibly intense...
Q: A flowerpot falls off a windowsill and falls past the window below. You may ignore air resistance. I...
A: Write the kinematic relation for distance travelled
Q: In 1816, Robert Stirling, a Scottish clergyman, patented the Stirling engine, which has found a wide...
A: Hi,there are multiple sub-parts in the question , as per our guidelines we are supposed to answer on...
Q: What is the best example of differential calculus in physics?
A: One of the best example of differential calculus in Physics is the Schrodinger equation in quantum m...
Q: Positive charge Q is distributed uniformly along the x-axis from x=0 to x=a. A positive point charge...
A: The charge Q is uniformly distributed along the axis x = 0 to x = a. The linear charge density of th...
Q: At what radius in Angstroms does the probability of finding an electron at a point in the ground sta...
A: Wave function of hydrogen atom for ground state is given by:
Q: Locate the radial distance of the radial nodes in the 3s orbital of an H atom.a.) node closest to nu...
A: The expression for the radial wave function of a 3s orbital of a hydrogen atom is given by,
Q: I asked this questions days before. It was shown as "answered"; however, there is no word in the sol...
A: Using Green’s theorem,
Q: Positive charge Q is distributed uniformly along the positive y-axis between y=0 and y=a. A negative...
A: The uniform charge distribution Q is along the positive y axis.
Q: A charge of -6.00 nC is spread uniformly over the surface of one face of a nonconducting disk of rad...
A: The surface charge density of the circular disc is
Q: Huck Finn walks at a speed of 0.60 m/s across his raft (that is, he walks perpendicular to the raft'...
A: The velocity of the person relative to the river bank is
Q: What is the photoelectric effect?
A: Photoelectric effect can be best understood by the photoelectric effect experiment. Photoelectric ef...
Q: A tree grows and increases in mass. Explain why this is not a violation of the law of conservation o...
A: A Tree has its foundation deep rooted beneath the earth where it is able to absorb water and nutrien...
Q: When asked for the altitude for the moon would I use arc degrees to measure that?
A: the altitude of the moon is measured from the horizon to the point where the center of the moon exis...
Q: In the first problem from the activity we found that the rate of change of energy with respect to ti...
A: Denote the potential energy of an object oscillating on a spring stretched a distance x from equilib...
Q: To explain the daily and yearly motions of the heavens, ancient astronomers imagined that the sun, m...
A: Ancient astronomers believed that the stars, sun, and moon were all fixed to concentric spheres that...
Q: Show that the total energy eigenfunctions ψ210(r,θ,φ) and ψ211(r,θ,φ) are orthogonal. Do you have to...
A: The total energy eigen functions of Ψ210(r, θ, Φ) and Ψ211(r, θ, Φ) can be calculated using followin...
Q: Two speedboats are traveling at the same speed relative to the water in opposite directions in a mov...
A: Let’s assume the velocity be
Q: A particle moves along a straight line such that its acceleration isa= (4t^2-4) m/s^2, where t is in...
A: Acceleration of the particle as a function of time is given by the equation:a = (4t2-4) m/s2We can f...
Q: What is the purpose of the Schrodinger equation? What is it used for?
A: In quantum systems, a wave function represents the probability amplitude of a quantum system to be f...
Q: State the total number of quantum states available to an electron in the levels in a hydrogen atom t...
A: In the above problem it is assumed that the expression for the energy of an electron in a hydrogen a...
Q: A textbook of mass 2.08 kg rests on a frictionless, horizontal surface. A cord attached to the book ...
A: Since, the both the books are attached with a same cord, these books move with same speed having sam...
Q: Charged Particle in Crossed E and B Fields A charged particle of mass m and positive charge q moves ...
A: (a)Electric field points in the y direction and magnetic field points in the z- direction. The net f...
Q: (10% ) Problem 7: An infinite conducting cylindrical shell of outer radius ri-0.10 m and inner radiu...
A: Given:
Q: Additional Materials еВook 0/1 points I Previous Answers OSUniPhys1 6.P105. 3/5 Submissions Used A 5...
A:
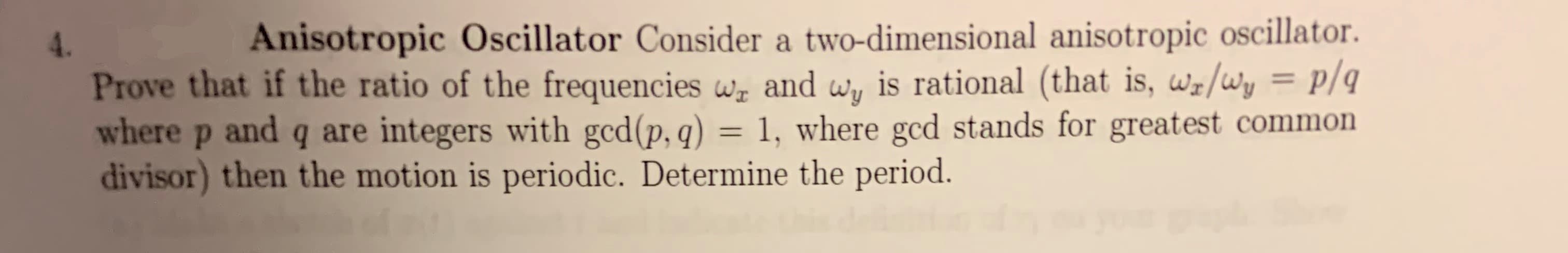
Trending now
This is a popular solution!
Step by step
Solved in 5 steps with 4 images
