At $0.41 per bushel, the daily supply for wheat is 402 bushels, and the daily demand is 565 bushels. When the price is raised to $0.80 per bushel, the daily supply increases to 532 bushels, and the daily demand decreases to 175 bushels. Assume that the price-supply and price-demand equations are linear. a. Find the price-supply equation. p = (Type an expression using q as the variable. Round to three decimal places as needed.) b. Find the price-demand equation p = (Type an expression using q as the variable. Round to three decimal places as needed.) c. Find the equilibrium price and equilibrium quantity price $ (Round to the nearest cent as needed.) quantity bushels (Round to the nearest bushel as needed.) d. Graph the two equations in the same coordinate system and identify the equilibrium point E, supply curve S, and demand curve D. Select the correct graph below Ос. ОА. В. D. None of the above Ap 1.2 Ар 1.2 1.2 D q q 0- 0 0- 0 E700 700 700 --E
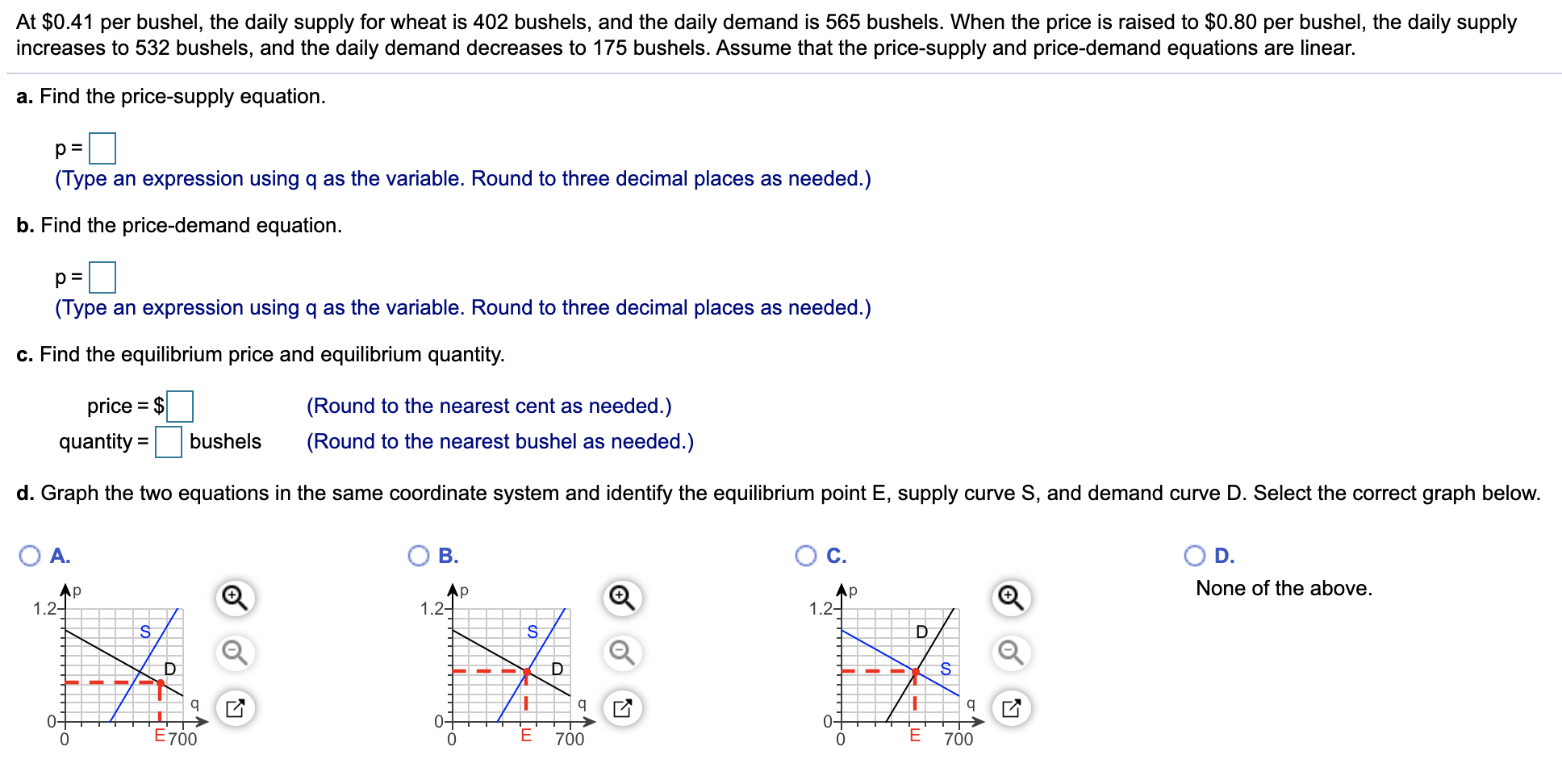
Image Transcriptionclose
At $0.41 per bushel, the daily supply for wheat is 402 bushels, and the daily demand is 565 bushels. When the price is raised to $0.80 per bushel, the daily supply increases to 532 bushels, and the daily demand decreases to 175 bushels. Assume that the price-supply and price-demand equations are linear. a. Find the price-supply equation. p = (Type an expression using q as the variable. Round to three decimal places as needed.) b. Find the price-demand equation p = (Type an expression using q as the variable. Round to three decimal places as needed.) c. Find the equilibrium price and equilibrium quantity price $ (Round to the nearest cent as needed.) quantity bushels (Round to the nearest bushel as needed.) d. Graph the two equations in the same coordinate system and identify the equilibrium point E, supply curve S, and demand curve D. Select the correct graph below Ос. ОА. В. D. None of the above Ap 1.2 Ар 1.2 1.2 D q q 0- 0 0- 0 E700 700 700 --E
Expert Answer
Related Algebra Q&A
Q: solve system of equations using substitution method. x+y=-6 xy=-40
A: The given system of equation is as below.x + y = – 6 ….(i)xy = – 40 ….(ii)
Q: Find a formula for the quadratic function whose graph has its vertex at (5,2) and its y-intercept at...
A: Find a formula for the quadratic function whose graph has its vertex at (5,2) and its y-intercept at...
Q: Landon Wallin is an auto mechanic who wishes to start his own business. He will need $4300 to purcha...
A: Formula used:
Q: Practice question 7.3
A: a) The slope of AB is evaluated and the slope intercept form is obtained as follows.
Q: The income I of a computer analyst varies directly as the number of hours h worked. If the analyst e...
A: Given income l is directly varies as the number of hours hIf $336 for working 8h.How much will the a...
Q: Simplify the radical expression. Assume that all variables represent positive real numbers. V98k798
A: Given that
Q: Solve the linear programming problem. Maximize and minimize P 5x9y subject to x+y 3 x+ 2y 4 4х + 5y ...
A: The given inequalities are
Q: (1/64)3n x 8 =26
A: Formula:
Q: Solve the equation for x. log4(x + 2) − log4(x) = log4(50)
A: Given:
