Homework Help is Here – Start Your Trial Now!
Math
Calculus
Because of past use of leaded gasoline, the concentration of lead in soil can be associated with how close the soil is to a heavily traveled road. The table shows average lead concentrations in parts per million of samples taken from different distances from roads.t Lead Concentration in Soil Near Roads Distance, x (meters) Lead, L (ppm) 90 10 60 15 40 20 32 (a) Find a log model for these data. (Round all numerical values to three decimal places.) 5 SxS 20 L(x) = ppm is the concentration of lead in the soil x meters from a heavily traveled road (b) An apartment complex has a dirt play area located 8 meters from a road. Calculate the lead concentration in the soil of the play area. (Round your answer to the nearest integer.) L(8) = ppm (c) Find an exponential model for the data. Compare this model to the log model found in part (a). (Round all numerical values to three decimal places.) 5

Because of past use of leaded gasoline, the concentration of lead in soil can be associated with how close the soil is to a heavily traveled road. The table shows average lead concentrations in parts per million of samples taken from different distances from roads.t Lead Concentration in Soil Near Roads Distance, x (meters) Lead, L (ppm) 90 10 60 15 40 20 32 (a) Find a log model for these data. (Round all numerical values to three decimal places.) 5 SxS 20 L(x) = ppm is the concentration of lead in the soil x meters from a heavily traveled road (b) An apartment complex has a dirt play area located 8 meters from a road. Calculate the lead concentration in the soil of the play area. (Round your answer to the nearest integer.) L(8) = ppm (c) Find an exponential model for the data. Compare this model to the log model found in part (a). (Round all numerical values to three decimal places.) 5

Algebra & Trigonometry with Analytic Geometry
Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter5: Inverse, Exponential, And Logarithmic Functions
Section: Chapter Questions
Problem 15DE
See similar textbooks
icon
Related questions
Question
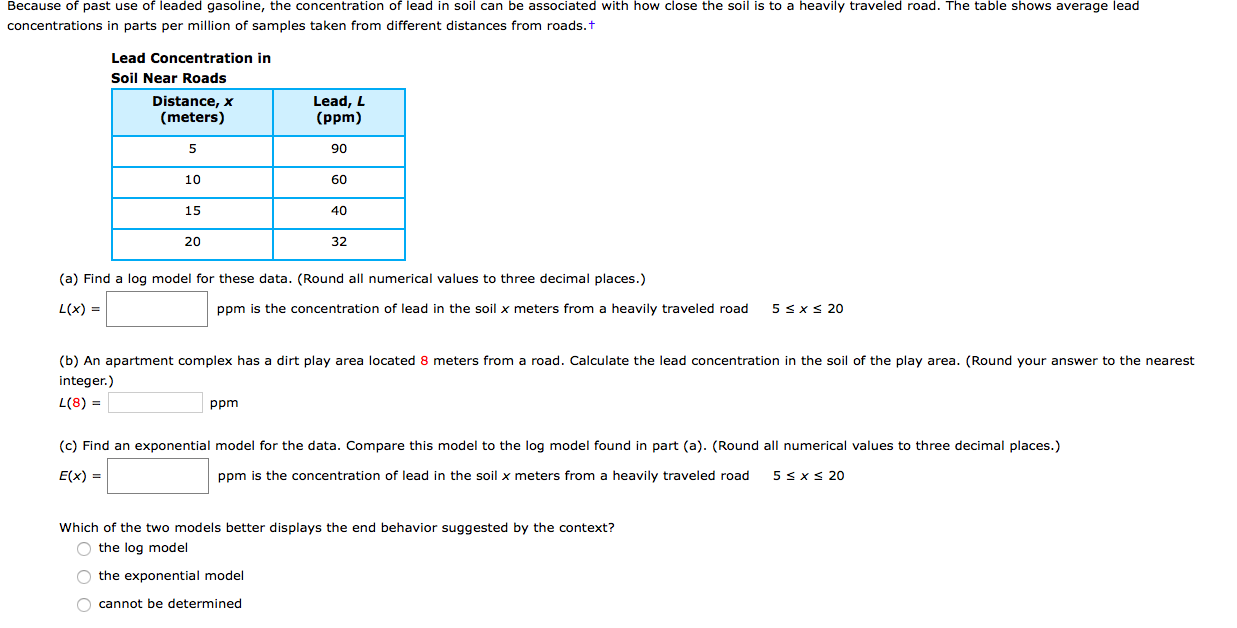
Because of past use of leaded gasoline, the concentration of lead in soil can be associated with how close the soil is to a heavily traveled road. The table shows average lead concentrations in parts per million of samples taken from different distances from roads.t Lead Concentration in Soil Near Roads Distance, x (meters) Lead, L (ppm) 90 10 60 15 40 20 32 (a) Find a log model for these data. (Round all numerical values to three decimal places.) 5 SxS 20 L(x) = ppm is the concentration of lead in the soil x meters from a heavily traveled road (b) An apartment complex has a dirt play area located 8 meters from a road. Calculate the lead concentration in the soil of the play area. (Round your answer to the nearest integer.) L(8) = ppm (c) Find an exponential model for the data. Compare this model to the log model found in part (a). (Round all numerical values to three decimal places.) 5 <x< 20 E(x) = ppm is the concentration of lead in the soil x meters from a heavily traveled road Which of the two models better displays the end behavior suggested by the context? O the log model O the exponential model O cannot be determined
Transcribed Image Text:Because of past use of leaded gasoline, the concentration of lead in soil can be associated with how close the soil is to a heavily traveled road. The table shows average lead concentrations in parts per million of samples taken from different distances from roads.t Lead Concentration in Soil Near Roads Distance, x (meters) Lead, L (ppm) 90 10 60 15 40 20 32 (a) Find a log model for these data. (Round all numerical values to three decimal places.) 5 SxS 20 L(x) = ppm is the concentration of lead in the soil x meters from a heavily traveled road (b) An apartment complex has a dirt play area located 8 meters from a road. Calculate the lead concentration in the soil of the play area. (Round your answer to the nearest integer.) L(8) = ppm (c) Find an exponential model for the data. Compare this model to the log model found in part (a). (Round all numerical values to three decimal places.) 5 <x< 20 E(x) = ppm is the concentration of lead in the soil x meters from a heavily traveled road Which of the two models better displays the end behavior suggested by the context? O the log model O the exponential model O cannot be determined
Expert Solution
trending now

Trending now

This is a popular solution!

steps

Step by step

Solved in 1 steps

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Algebra & Trigonometry with Analytic Geometry
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage
College Algebra
College Algebra
Algebra
ISBN:
9781938168383
Author:
Jay Abramson
Publisher:
OpenStax
College Algebra (MindTap Course List)
College Algebra (MindTap Course List)
Algebra
ISBN:
9781305652231
Author:
R. David Gustafson, Jeff Hughes
Publisher:
Cengage Learning
College Algebra
College Algebra
Algebra
ISBN:
9781337282291
Author:
Ron Larson
Publisher:
Cengage Learning
Functions and Change: A Modeling Approach to Coll…
Functions and Change: A Modeling Approach to Coll…
Algebra
ISBN:
9781337111348
Author:
Bruce Crauder, Benny Evans, Alan Noell
Publisher:
Cengage Learning
SEE MORE TEXTBOOKS