c and Those complex num black, while those that lead to un used similar ideas to generate his own recurs The image "i of the storm" reproduced here function the is based f(2) = (1-i)z*+(7+1)z where again z is a 2z +6 %3D variable that will be replaced with complex numbers. The image is actually a picture of the complex plane, with the origin in the very center of the golden ring. The golden ring consists of those complex numbers that lie a distance between 0.9 and 1.1 units from the origin. The rules for coloring other complex numbers in the plane are as follows: given an initial complex number z not on the gold ring, f(z) is calculated. If the complex number f(z) lies somewhere on the gold ring, the original number z is colored the deepest shade of green. If not, the iterate f (z) is calculated. If this result lies in the gold ring, the original z is colored a bluish shade of green. If not, the process continues up to the 12th iterate f (z), using a different color time. If f" (z) lies in the gold ring, z is colored red, and if not the process halts and z is colored black. The idea of recursion can be used to generate any number of similar images, with the end result usually striking and often surprising even to the creator. Exercises In each of the following problems, use the information given to determine a. (f + g)(-1). f b. (f -g)(-1),c. (fg)(-1), and d. (4) -(-1). See Examples 1,2, and 3. 1. f(-1)=-3 and g(-1)=5 2. f(-1)=0 and g(-1)=-1 3. f(x)=x² – 3 and g(x)= x %3D 4. f(x)= Vx and g(x)= x – 1 5. f(-1)= 15 and g(-1)=-3 6. f(x)= and g(x)= 6x %3D %3D 7. f(x)=x* +1 and g(x) = x" +2 %3D 8. f(x)=, 6-X and g(x) = %3D 9. f={(5, 2).(0, – 1).(-1, 3).(-2, 4)} and g = {(-1, 3).(0, 5)} -4 %3D 10. f = {(3,15).(2, – 1).(-1, 1)} and g(x)= -2 283 Combining Functions Section 3.6 11. 12. 4. 4 2 -2 -2 -4 -4 -4 -2 0 2 4 -4 -2 2 4 13. 14. 4 4 0+ 0+ -2 -2 -4 -4 -4 -2 0 -4 -2 4 In each of the following problems, find a. the formula and domain for f+ g, and b. the formula and domain for See Examples 2 and 3. 15. f(x)=|x| and g (x) = Vx 16. f(x) = x² -1 and g(x)= {x %3D 3 17. f(x)=x-1 and g(x) = x² – 1 18. f(x)= x² and g (x)= x – 3 19. f(x) = 3x and g(x)= x' –8 20. f(x) = x² +4 and g (x) = /x – 2 2 21. f(x)=-2x² and g(x)=|x+4| 22. f (x)= 6x – 1 and g (x) = x³ 4- ఉం 2. 2. 2.
c and Those complex num black, while those that lead to un used similar ideas to generate his own recurs The image "i of the storm" reproduced here function the is based f(2) = (1-i)z*+(7+1)z where again z is a 2z +6 %3D variable that will be replaced with complex numbers. The image is actually a picture of the complex plane, with the origin in the very center of the golden ring. The golden ring consists of those complex numbers that lie a distance between 0.9 and 1.1 units from the origin. The rules for coloring other complex numbers in the plane are as follows: given an initial complex number z not on the gold ring, f(z) is calculated. If the complex number f(z) lies somewhere on the gold ring, the original number z is colored the deepest shade of green. If not, the iterate f (z) is calculated. If this result lies in the gold ring, the original z is colored a bluish shade of green. If not, the process continues up to the 12th iterate f (z), using a different color time. If f" (z) lies in the gold ring, z is colored red, and if not the process halts and z is colored black. The idea of recursion can be used to generate any number of similar images, with the end result usually striking and often surprising even to the creator. Exercises In each of the following problems, use the information given to determine a. (f + g)(-1). f b. (f -g)(-1),c. (fg)(-1), and d. (4) -(-1). See Examples 1,2, and 3. 1. f(-1)=-3 and g(-1)=5 2. f(-1)=0 and g(-1)=-1 3. f(x)=x² – 3 and g(x)= x %3D 4. f(x)= Vx and g(x)= x – 1 5. f(-1)= 15 and g(-1)=-3 6. f(x)= and g(x)= 6x %3D %3D 7. f(x)=x* +1 and g(x) = x" +2 %3D 8. f(x)=, 6-X and g(x) = %3D 9. f={(5, 2).(0, – 1).(-1, 3).(-2, 4)} and g = {(-1, 3).(0, 5)} -4 %3D 10. f = {(3,15).(2, – 1).(-1, 1)} and g(x)= -2 283 Combining Functions Section 3.6 11. 12. 4. 4 2 -2 -2 -4 -4 -4 -2 0 2 4 -4 -2 2 4 13. 14. 4 4 0+ 0+ -2 -2 -4 -4 -4 -2 0 -4 -2 4 In each of the following problems, find a. the formula and domain for f+ g, and b. the formula and domain for See Examples 2 and 3. 15. f(x)=|x| and g (x) = Vx 16. f(x) = x² -1 and g(x)= {x %3D 3 17. f(x)=x-1 and g(x) = x² – 1 18. f(x)= x² and g (x)= x – 3 19. f(x) = 3x and g(x)= x' –8 20. f(x) = x² +4 and g (x) = /x – 2 2 21. f(x)=-2x² and g(x)=|x+4| 22. f (x)= 6x – 1 and g (x) = x³ 4- ఉం 2. 2. 2.
Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter4: Polynomial And Rational Functions
Section: Chapter Questions
Problem 21RE
Related questions
Question
I need questions 12,13,17,20

Transcribed Image Text:c and
Those complex num
black, while those that lead to un
used similar ideas to generate his own recurs
The image "i of the storm" reproduced
here
function
the
is
based
f(2) = (1-i)z*+(7+1)z where again z is a
2z +6
%3D
variable that will be replaced with complex
numbers. The image is actually a picture of
the complex plane, with the origin in the
very center of the golden ring. The golden
ring consists of those complex numbers
that lie a distance between 0.9 and 1.1 units
from the origin. The rules for coloring
other complex numbers in the plane are as
follows: given an initial complex number z
not on the gold ring, f(z) is calculated. If
the complex number f(z) lies somewhere on the gold ring, the original number z is
colored the deepest shade of green. If not, the iterate f (z) is calculated.
If this result lies in the gold ring, the original z is colored a bluish shade of green. If
not, the process continues up to the 12th iterate f (z), using a different color
time. If f" (z) lies in the gold ring, z is colored red, and if not the process halts and z
is colored black.
The idea of recursion can be used to generate any number of similar images, with the
end result usually striking and often surprising even to the creator.
Exercises
In each of the following problems, use the information given to determine a. (f + g)(-1).
f
b. (f -g)(-1),c. (fg)(-1), and d.
(4)
-(-1). See Examples 1,2, and 3.
1. f(-1)=-3 and g(-1)=5
2. f(-1)=0 and g(-1)=-1
3. f(x)=x² – 3 and g(x)= x
%3D
4. f(x)= Vx and g(x)= x – 1
5. f(-1)= 15 and g(-1)=-3
6. f(x)=
and g(x)= 6x
%3D
%3D
7. f(x)=x* +1 and g(x) = x" +2
%3D
8. f(x)=,
6-X
and g(x) =
%3D
9. f={(5, 2).(0, – 1).(-1, 3).(-2, 4)} and g = {(-1, 3).(0, 5)}
-4
%3D
10. f = {(3,15).(2, – 1).(-1, 1)} and g(x)= -2
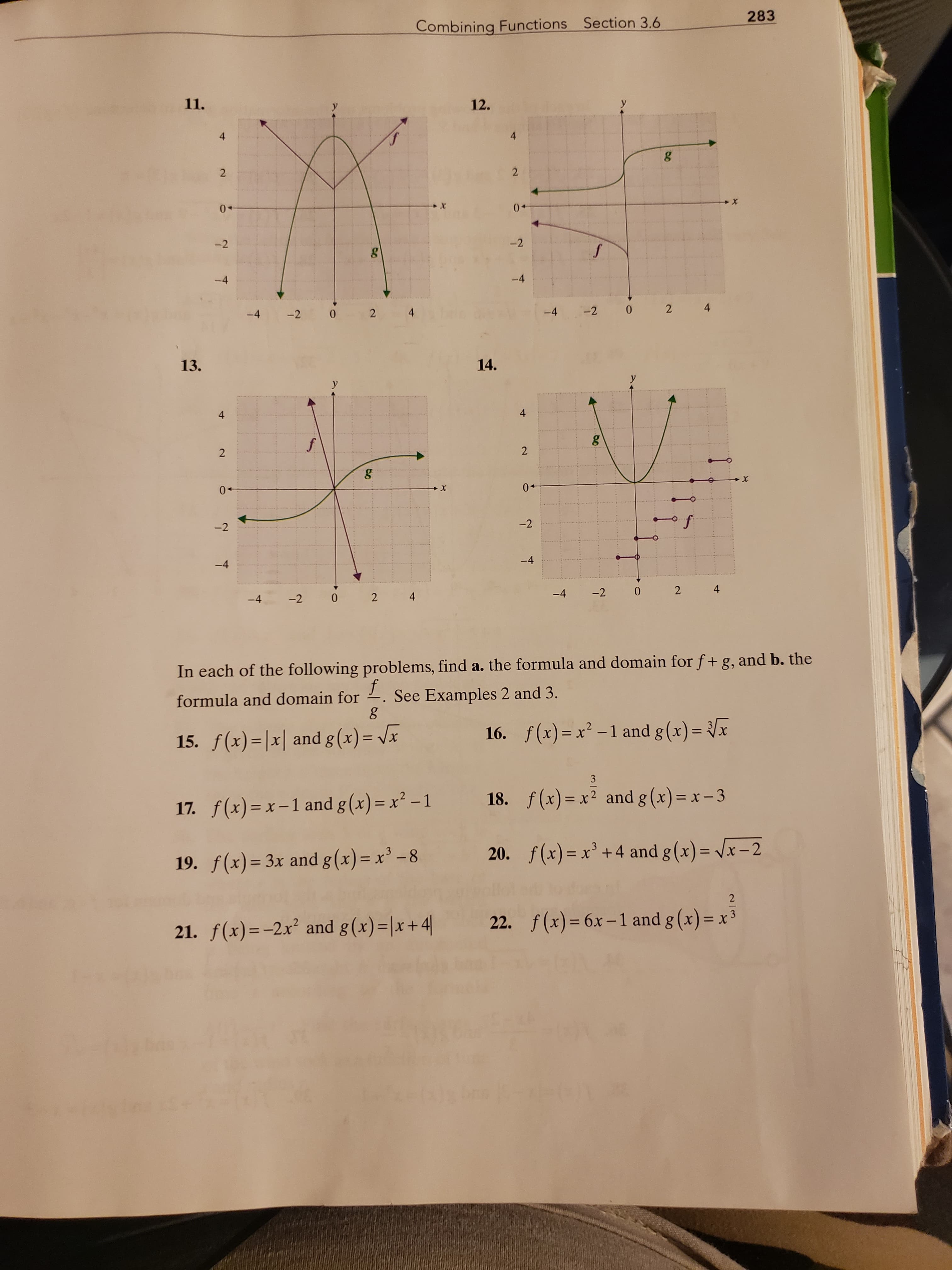
Transcribed Image Text:283
Combining Functions Section 3.6
11.
12.
4.
4
2
-2
-2
-4
-4
-4
-2 0
2
4
-4
-2
2 4
13.
14.
4
4
0+
0+
-2
-2
-4
-4
-4
-2 0
-4
-2
4
In each of the following problems, find a. the formula and domain for f+ g, and b. the
formula and domain for
See Examples 2 and 3.
15. f(x)=|x| and g (x) = Vx
16. f(x) = x² -1 and g(x)= {x
%3D
3
17. f(x)=x-1 and g(x) = x² – 1
18. f(x)= x² and g (x)= x – 3
19. f(x) = 3x and g(x)= x' –8
20. f(x) = x² +4 and g (x) = /x – 2
2
21. f(x)=-2x² and g(x)=|x+4|
22. f (x)= 6x – 1 and g (x) = x³
4-
ఉం
2.
2.
2.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 3 steps with 3 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Recommended textbooks for you

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage