Chapter 11, Problem 067 The figure is an overhead view of a thin uniform rod of length 0.690 m and mass M rotating horizontally at 82.0 rad/s counterclockwise about an axis through its center. A particle of mass M/3.20 and traveling horizontally at speed 43.0 m/s hits the rod and sticks. The particle's path is perpendicular to the rod at the instant of the hit, at a distance d from the rod's center. (a) At what value of d are rod and particle stationary after the hit? (b) In which direction do rod and particle rotate if d is greater than this value? Rotation axis Particle (a) Number Units (b) Use correct number of significant digits; the tolerance is +/-2%
Chapter 11, Problem 067 The figure is an overhead view of a thin uniform rod of length 0.690 m and mass M rotating horizontally at 82.0 rad/s counterclockwise about an axis through its center. A particle of mass M/3.20 and traveling horizontally at speed 43.0 m/s hits the rod and sticks. The particle's path is perpendicular to the rod at the instant of the hit, at a distance d from the rod's center. (a) At what value of d are rod and particle stationary after the hit? (b) In which direction do rod and particle rotate if d is greater than this value? Rotation axis Particle (a) Number Units (b) Use correct number of significant digits; the tolerance is +/-2%
University Physics Volume 1
18th Edition
ISBN:9781938168277
Author:William Moebs, Samuel J. Ling, Jeff Sanny
Publisher:William Moebs, Samuel J. Ling, Jeff Sanny
Chapter11: Angular Momentum
Section: Chapter Questions
Problem 89AP: A solid cylinder of mass 2.0 kg and radius 20 cm is rotating counterclockwise around a vertical axis...
Related questions
Question
100%
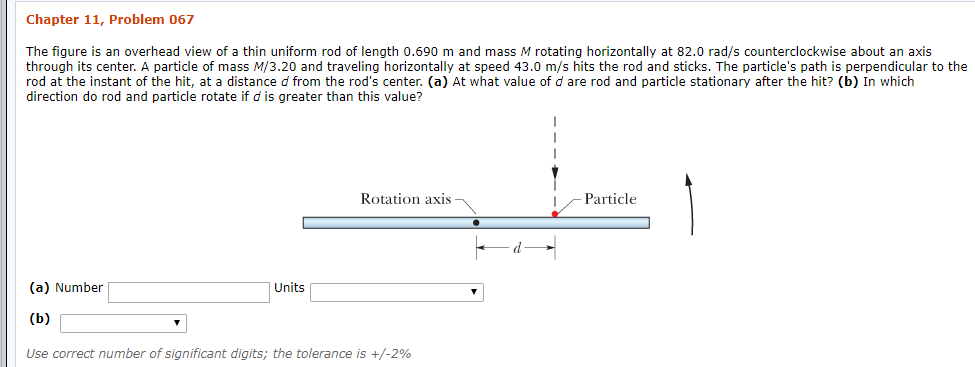
Transcribed Image Text:Chapter 11, Problem 067
The figure is an overhead view of a thin uniform rod of length 0.690 m and mass M rotating horizontally at 82.0 rad/s counterclockwise about an axis
through its center. A particle of mass M/3.20 and traveling horizontally at speed 43.0 m/s hits the rod and sticks. The particle's path is perpendicular to the
rod at the instant of the hit, at a distance d from the rod's center. (a) At what value of d are rod and particle stationary after the hit? (b) In which
direction do rod and particle rotate if d is greater than this value?
Rotation axis
Particle
(a) Number
Units
(b)
Use correct number of significant digits; the tolerance is +/-2%
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 1 images

Recommended textbooks for you

University Physics Volume 1
Physics
ISBN:
9781938168277
Author:
William Moebs, Samuel J. Ling, Jeff Sanny
Publisher:
OpenStax - Rice University

Principles of Physics: A Calculus-Based Text
Physics
ISBN:
9781133104261
Author:
Raymond A. Serway, John W. Jewett
Publisher:
Cengage Learning

Physics for Scientists and Engineers, Technology …
Physics
ISBN:
9781305116399
Author:
Raymond A. Serway, John W. Jewett
Publisher:
Cengage Learning

University Physics Volume 1
Physics
ISBN:
9781938168277
Author:
William Moebs, Samuel J. Ling, Jeff Sanny
Publisher:
OpenStax - Rice University

Principles of Physics: A Calculus-Based Text
Physics
ISBN:
9781133104261
Author:
Raymond A. Serway, John W. Jewett
Publisher:
Cengage Learning

Physics for Scientists and Engineers, Technology …
Physics
ISBN:
9781305116399
Author:
Raymond A. Serway, John W. Jewett
Publisher:
Cengage Learning

Physics for Scientists and Engineers: Foundations…
Physics
ISBN:
9781133939146
Author:
Katz, Debora M.
Publisher:
Cengage Learning

Classical Dynamics of Particles and Systems
Physics
ISBN:
9780534408961
Author:
Stephen T. Thornton, Jerry B. Marion
Publisher:
Cengage Learning