Dumatis of the Soivent 4moleculos of the solvent wmagıne you nove moreccilos above, draKI the mD1ecLuIar Streictiure Of by considering the salvents togther IMFS
Question b

The given solvent molecule is represented as follows:
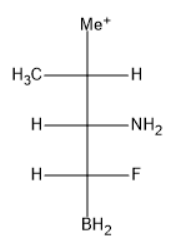
The forces which provide interaction including force of repulsion and attraction acting between the neighboring particles and molecules is known as intermolecular force.
Different types of intermolecular forces are known for example, London forces or dispersion forces, hydrogen bond, dipole-dipole forces, ion-dipole forces etc.
The bond formed between the hydrogen atom and an electronegative atom like nitrogen, oxygen, and fluorine is termed as hydrogen bonding.
Hydrogen bonding is of two types one is intermolecular hydrogen bonding, and other is intramolecular hydrogen bonding.
The hydrogen bond formed between the same or different molecules is termed as intermolecular hydrogen bonding.
Step by step
Solved in 4 steps with 3 images









