Business
Engineering
Math
Science
Social Scienceeh the directional derivative ofxy at the point (2, 1) has the value 2.29. Find all points at which the direction of fastest change of thefunction f(x, y)= x2 + y - 2x -4y is i +30. Near a buoy, the
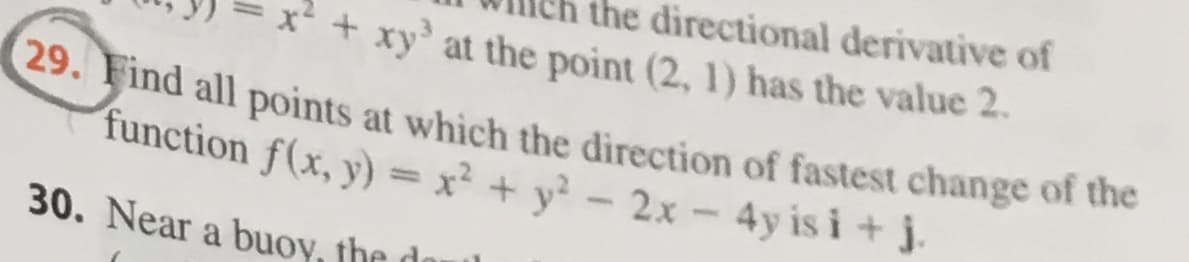
Image Transcriptionclose
eh the directional derivative of xy at the point (2, 1) has the value 2. 29. Find all points at which the direction of fastest change of the function f(x, y)= x2 + y - 2x -4y is i + 30. Near a buoy, the
Expert Answer
Given function
Image Transcriptionclose
f(x, y) x2 - 2x 4y To find: all points at which the direction of the fastest change of function is i+j
Note:
Image Transcriptionclose
A scalar field fwill have its maximum rate of change in the direction of its gradient vector. Therefore, we find all points (x, y) where the gradient i.e. Vf(x, y) is parallel to i+j
Calculatin...
Image Transcriptionclose
Vf(x, y) (2y - 4)j = ki + kj, for some k> 0, giving 2x - 2 2y -4 (2x- 2)i + (2y 4)j Thus, (2x 2)i Or y x
Math
Calculus
Other
Related Calculus Q&A
Q: Verify that the function f(x)= x-3x+2 satisfies the hypotheses of the Mean Value Theorem 6. on the i...
A: Known fact:
Q: Find the minimum or maximum value of the function f(x) x2x2 7 а. 4 3 b. 4 7 с. A-2) 4 d. 7 2 e. 7 2
A: Given:
Q: A rectangle is constructed with its base on the x-axis and its upper two vertices on the parabola y...
A: Given informationRectangle base is on x axisTop on parabola
Q: Exercise 6: Use Taylor's theorem to evaluate the following limits (а) lim 0 cos(x)1+ x2 /2 3 sin2(ar...
A: Part (a):Evaluate limit using Taylor’s theorem.
Q: can u help me with this Jacobian question please
A: Given transformation is
Q: Given y=5 sin(4x – π), state the(a) period (b) phase shift
A: To determine:Part a) periodPart b) phase shift
Q: Find the limit. Use l'Hospital's Rule if appropriate. If there is a more elementary method, consider...
A: Given:
Q: Estimate the area under the graph of f(x) = 10 cos(x) from x = 0 to x = π/2 using four approximating...
A: Consider the given function:
Q: Solve the given equation. (Enter your answers as a comma-separated list. Let k be any integer. Round...
A: Given:
