Excercise 1: Controller design. The block diagram for an aircraft's attitude control system is shown below Controller Plant 2s 4 y е u С(8) 82 0.1s4 п We will attempt to design a controller that meets the following specifications: Rise time of less than 1.2 seconds Settling time of less than 4 seconds Steady-state error less than 1%, for a step input For sensor-noise rejection reasons, the controller's gain cannot exceed 10 (a) Find the (closed-loop) transfer function from r to y, for a proportional controller C(s) = kp (b) Translate the given specifications into constraints on the values of 5, wn, and a, for a standard second-order system. (c) Sketch by hand the root locus for the purely proportional controller. Please briefly explain the rules you applied to obtain your sketch, and show calculations for any asymptotes. (d) What range of kp values are allowed such that all requirements are satisfied except steady-state error? Mark on the root locus plots from part (c) the points that correspond to these values of kp. (e) Find an expression for the steady-state error. Can you find a purely proportional controller that meets all of the specifications? If so, find a suitable value of k,; if not, find the "best" value of k, that you can. Justify your interpretation of "best." Use Matlab to plot the step response for the closed-loop system, and verify that the response agrees with your predictions. (f) Now consider an integral controller, C(s) = ki/s. Find the transfer function from r to y and sketch the root locus with respect to ki for this system. Please briefly explain the rules you applied to obtain your sketch, and show calculations for any asymptotes.
Excercise 1: Controller design. The block diagram for an aircraft's attitude control system is shown below Controller Plant 2s 4 y е u С(8) 82 0.1s4 п We will attempt to design a controller that meets the following specifications: Rise time of less than 1.2 seconds Settling time of less than 4 seconds Steady-state error less than 1%, for a step input For sensor-noise rejection reasons, the controller's gain cannot exceed 10 (a) Find the (closed-loop) transfer function from r to y, for a proportional controller C(s) = kp (b) Translate the given specifications into constraints on the values of 5, wn, and a, for a standard second-order system. (c) Sketch by hand the root locus for the purely proportional controller. Please briefly explain the rules you applied to obtain your sketch, and show calculations for any asymptotes. (d) What range of kp values are allowed such that all requirements are satisfied except steady-state error? Mark on the root locus plots from part (c) the points that correspond to these values of kp. (e) Find an expression for the steady-state error. Can you find a purely proportional controller that meets all of the specifications? If so, find a suitable value of k,; if not, find the "best" value of k, that you can. Justify your interpretation of "best." Use Matlab to plot the step response for the closed-loop system, and verify that the response agrees with your predictions. (f) Now consider an integral controller, C(s) = ki/s. Find the transfer function from r to y and sketch the root locus with respect to ki for this system. Please briefly explain the rules you applied to obtain your sketch, and show calculations for any asymptotes.
Chapter47: Solid-state Adjustable Speed Control
Section: Chapter Questions
Problem 5SQ
Related questions
Question
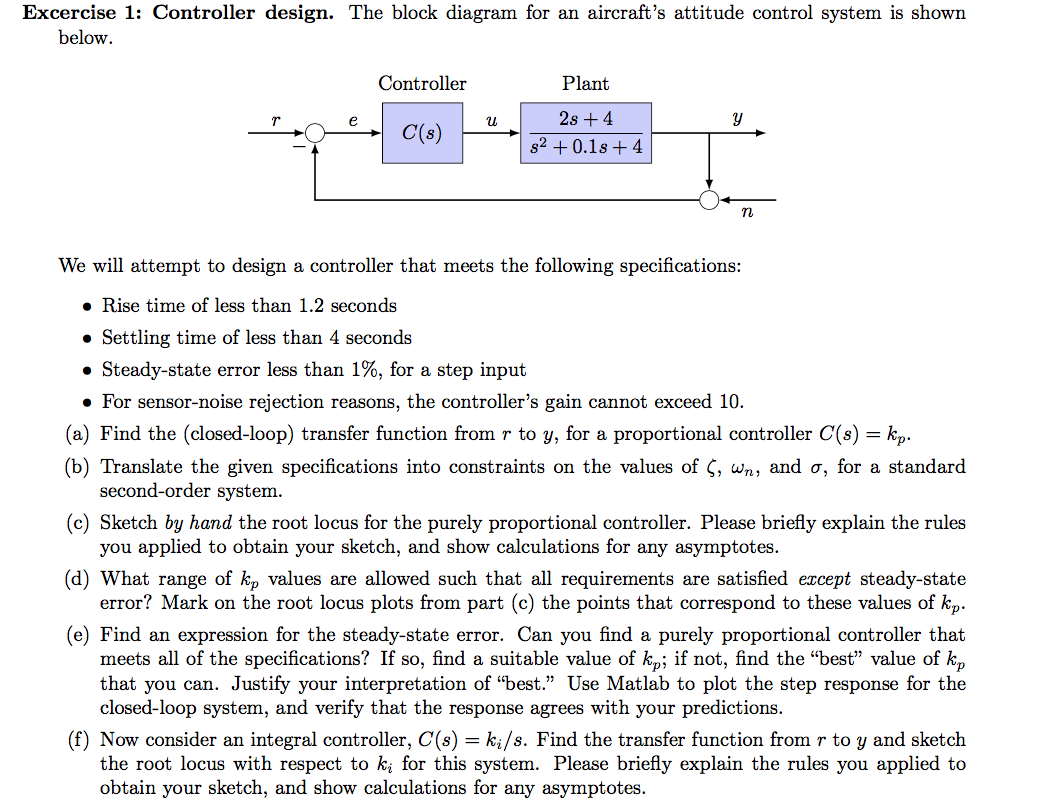
Transcribed Image Text:Excercise 1: Controller design. The block diagram for an aircraft's attitude control system is shown
below
Controller
Plant
2s 4
y
е
u
С(8)
82 0.1s4
п
We will attempt to design a controller that meets the following specifications:
Rise time of less than 1.2 seconds
Settling time of less than 4 seconds
Steady-state error less than 1%, for a step input
For sensor-noise rejection reasons, the controller's gain cannot exceed 10
(a) Find the (closed-loop) transfer function from r to y, for a proportional controller C(s) = kp
(b) Translate the given specifications into constraints on the values of 5, wn, and a, for a standard
second-order system.
(c) Sketch by hand the root locus for the purely proportional controller. Please briefly explain the rules
you applied to obtain your sketch, and show calculations for any asymptotes.
(d) What range of kp values are allowed such that all requirements are satisfied except steady-state
error? Mark on the root locus plots from part (c) the points that correspond to these values of kp.
(e) Find an expression for the steady-state error. Can you find a purely proportional controller that
meets all of the specifications? If so, find a suitable value of k,; if not, find the "best" value of k,
that you can. Justify your interpretation of "best." Use Matlab to plot the step response for the
closed-loop system, and verify that the response agrees with your predictions.
(f) Now consider an integral controller, C(s) = ki/s. Find the transfer function from r to y and sketch
the root locus with respect to ki for this system. Please briefly explain the rules you applied to
obtain your sketch, and show calculations for any asymptotes.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 8 steps with 7 images

Recommended textbooks for you

