Trigonometry (MindTap Course List)
10th Edition
ISBN:9781337278461
Author:Ron Larson
Publisher:Ron Larson
Chapter6: Topics In Analytic Geometry
Section6.2: Introduction To Conics: parabolas
Problem 4ECP: Find an equation of the tangent line to the parabola y=3x2 at the point 1,3.
Related questions
Question
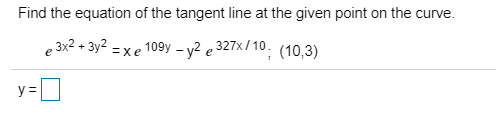
Transcribed Image Text:Find the equation of the tangent line at the given point on the curve.
109y2e 327x/10. (10,3)
, 3x2 + Зу2
= xe
e
у3
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 5 steps with 5 images

Recommended textbooks for you

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning