For the past decade, rubber powder has been used in asphalt cement to improve performance. An article includes a regression of y = axial strength (MPa) on x cube strength (MPa) based on the following sample data: 112.3 97.0 92.7 86.0 102.0 99.2 95.8 103.5 89.0 86.7 74.7 70.7 58.0 49.2 74.3 73.0 68.3 59.5 57.3 48.9 (a) Obtain the equation of the least squares line. (Round all numerical values to four decimal places.) %3D Interpret the slope. A one MPa decrease in axial strength is associated with an increase in the predicted cube strength equal to the slope. A one MPa decrease in cube strength is associated with an increase in the predicted axial strength equal to the slope. A one MPa increase in axial strength is associated with an increase in the predicted cube strength equal to the slope. A one MPa increase in cube strength is associated with an increase in the predicted axial strength equal to the slope. (b) Calculate the coefficient of determination. (Round your answer to four decimal places.) Interpret the coefficient of determination. The coefficient of determination is the proportion of the observed variation in axial strength of asphalt samples of this type that can be attributed to its linear relationship with cube strength. The coefficient of determination is the number of the observed samples of axial strength of asphalt that can be explained by variation in cube strength. The coefficient of determination is the proportion of the observed variation in axial strength of asphalt samples of this type that cannot be attributed to its linear relationship with cube strength. The coefficient of determination is the pumber of the observed samples of axial strenath of asohalt that cannot be explained by vadiation My Questions... renoth #DA0 ENG 917 PM Skype Chapter 12 - . e certified.pdf- TOSHIBA YGUR END WOME
For the past decade, rubber powder has been used in asphalt cement to improve performance. An article includes a regression of y = axial strength (MPa) on x cube strength (MPa) based on the following sample data: 112.3 97.0 92.7 86.0 102.0 99.2 95.8 103.5 89.0 86.7 74.7 70.7 58.0 49.2 74.3 73.0 68.3 59.5 57.3 48.9 (a) Obtain the equation of the least squares line. (Round all numerical values to four decimal places.) %3D Interpret the slope. A one MPa decrease in axial strength is associated with an increase in the predicted cube strength equal to the slope. A one MPa decrease in cube strength is associated with an increase in the predicted axial strength equal to the slope. A one MPa increase in axial strength is associated with an increase in the predicted cube strength equal to the slope. A one MPa increase in cube strength is associated with an increase in the predicted axial strength equal to the slope. (b) Calculate the coefficient of determination. (Round your answer to four decimal places.) Interpret the coefficient of determination. The coefficient of determination is the proportion of the observed variation in axial strength of asphalt samples of this type that can be attributed to its linear relationship with cube strength. The coefficient of determination is the number of the observed samples of axial strength of asphalt that can be explained by variation in cube strength. The coefficient of determination is the proportion of the observed variation in axial strength of asphalt samples of this type that cannot be attributed to its linear relationship with cube strength. The coefficient of determination is the pumber of the observed samples of axial strenath of asohalt that cannot be explained by vadiation My Questions... renoth #DA0 ENG 917 PM Skype Chapter 12 - . e certified.pdf- TOSHIBA YGUR END WOME
Functions and Change: A Modeling Approach to College Algebra (MindTap Course List)
6th Edition
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Bruce Crauder, Benny Evans, Alan Noell
Chapter5: A Survey Of Other Common Functions
Section5.6: Higher-degree Polynomials And Rational Functions
Problem 1TU: The following fictitious table shows kryptonite price, in dollar per gram, t years after 2006. t=...
Related questions
Question
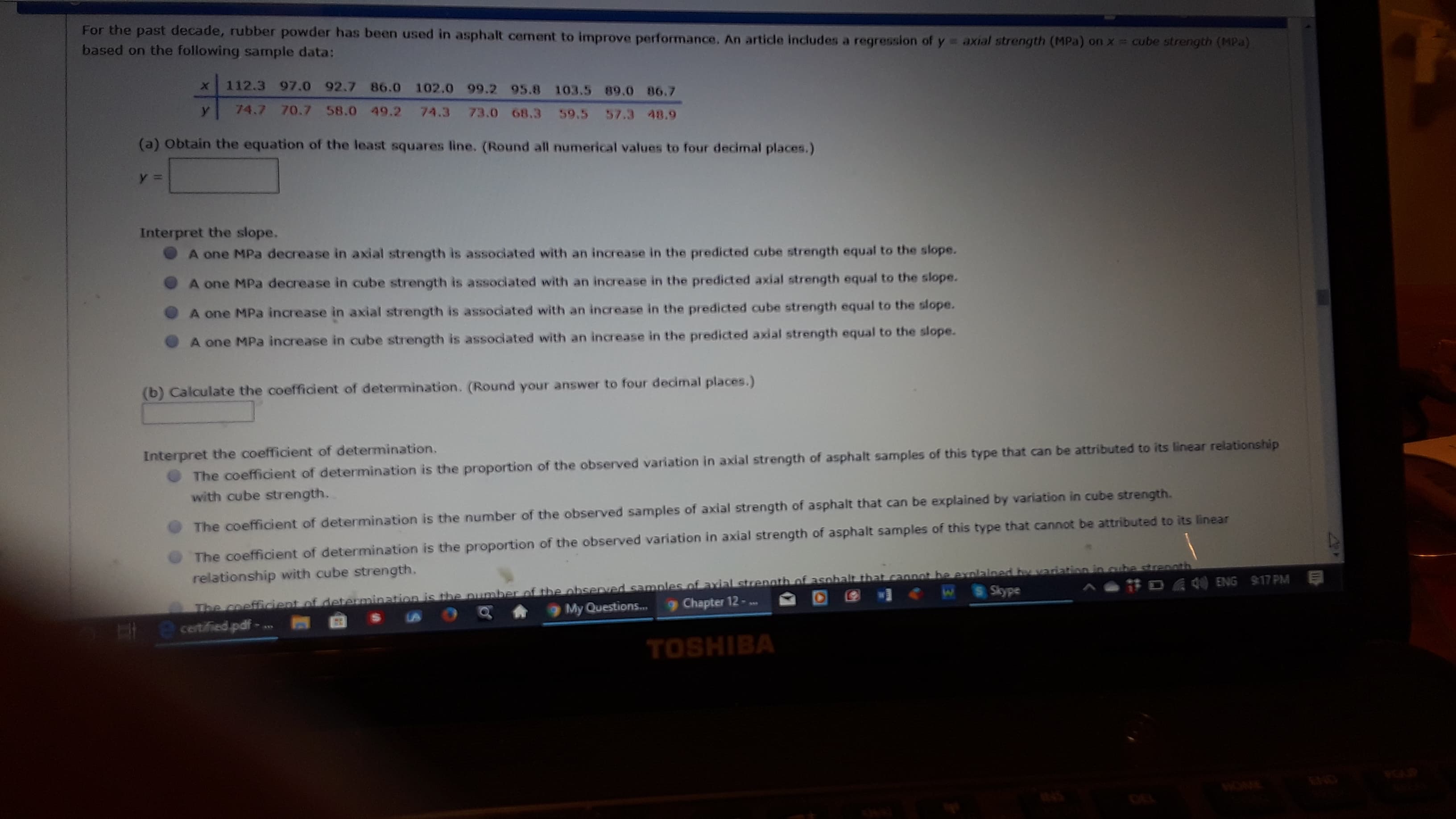
Transcribed Image Text:For the past decade, rubber powder has been used in asphalt cement to improve performance. An article includes a regression of y = axial strength (MPa) on x cube strength (MPa)
based on the following sample data:
112.3 97.0 92.7 86.0 102.0 99.2 95.8 103.5 89.0 86.7
74.7 70.7 58.0 49.2 74.3 73.0 68.3 59.5 57.3 48.9
(a) Obtain the equation of the least squares line. (Round all numerical values to four decimal places.)
%3D
Interpret the slope.
A one MPa decrease in axial strength is associated with an increase in the predicted cube strength equal to the slope.
A one MPa decrease in cube strength is associated with an increase in the predicted axial strength equal to the slope.
A one MPa increase in axial strength is associated with an increase in the predicted cube strength equal to the slope.
A one MPa increase in cube strength is associated with an increase in the predicted axial strength equal to the slope.
(b) Calculate the coefficient of determination. (Round your answer to four decimal places.)
Interpret the coefficient of determination.
The coefficient of determination is the proportion of the observed variation in axial strength of asphalt samples of this type that can be attributed to its linear relationship
with cube strength.
The coefficient of determination is the number of the observed samples of axial strength of asphalt that can be explained by variation in cube strength.
The coefficient of determination is the proportion of the observed variation in axial strength of asphalt samples of this type that cannot be attributed to its linear
relationship with cube strength.
The coefficient of determination is the pumber of the observed samples of axial strenath of asohalt that cannot be explained by vadiation
My Questions...
renoth
#DA0 ENG 917 PM
Skype
Chapter 12 - .
e certified.pdf-
TOSHIBA
YGUR
END
WOME
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 1 images

Recommended textbooks for you

Functions and Change: A Modeling Approach to Coll…
Algebra
ISBN:
9781337111348
Author:
Bruce Crauder, Benny Evans, Alan Noell
Publisher:
Cengage Learning

Glencoe Algebra 1, Student Edition, 9780079039897…
Algebra
ISBN:
9780079039897
Author:
Carter
Publisher:
McGraw Hill

Functions and Change: A Modeling Approach to Coll…
Algebra
ISBN:
9781337111348
Author:
Bruce Crauder, Benny Evans, Alan Noell
Publisher:
Cengage Learning

Glencoe Algebra 1, Student Edition, 9780079039897…
Algebra
ISBN:
9780079039897
Author:
Carter
Publisher:
McGraw Hill