If no 25 and nq 25, estimate P(fewer than 7) with n 14 rse approximation is not suitable. and p 0.6 by using the normal distribution as an approximation to the binomial distribution; if np< 5 or nq<5, then state that the normal Select the correct choice below and, if necessary, fill in the answer box to complete your ou choice O A. P(fewer than 7)= (Round to four decimal places as needed.) ign B. The normal approximation is not suitable. dy adel atCr Тext Click to select and enter your answer(s) and then click Check Answer hapt Check Answer Clear All All parts showing Tools fo OK 10:30 3 ^# 12/3 e Ot Type here to search
If no 25 and nq 25, estimate P(fewer than 7) with n 14 rse approximation is not suitable. and p 0.6 by using the normal distribution as an approximation to the binomial distribution; if np< 5 or nq<5, then state that the normal Select the correct choice below and, if necessary, fill in the answer box to complete your ou choice O A. P(fewer than 7)= (Round to four decimal places as needed.) ign B. The normal approximation is not suitable. dy adel atCr Тext Click to select and enter your answer(s) and then click Check Answer hapt Check Answer Clear All All parts showing Tools fo OK 10:30 3 ^# 12/3 e Ot Type here to search
MATLAB: An Introduction with Applications
6th Edition
ISBN:9781119256830
Author:Amos Gilat
Publisher:Amos Gilat
Chapter1: Starting With Matlab
Section: Chapter Questions
Problem 1P
Related questions
Question
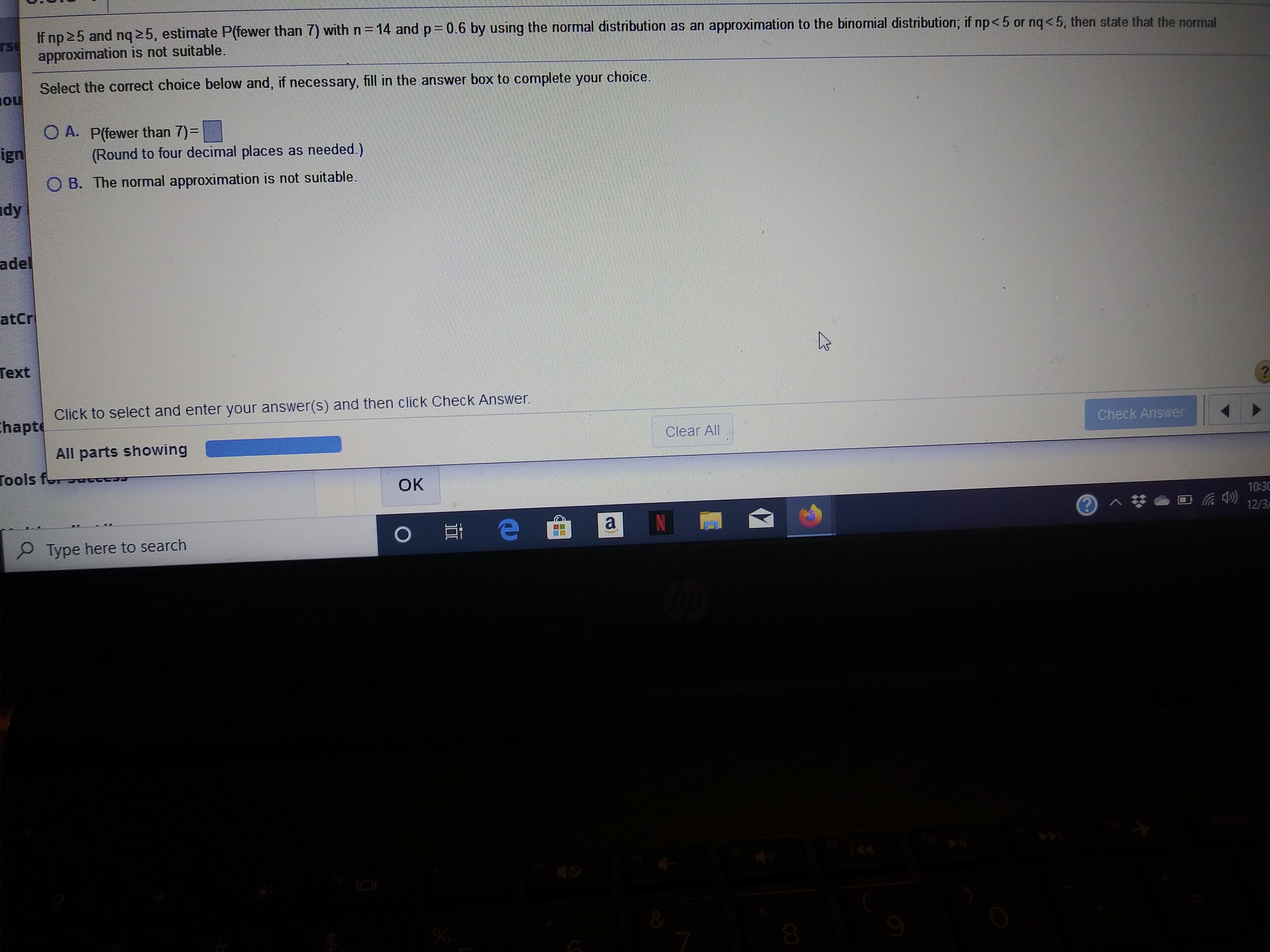
Transcribed Image Text:If no 25 and nq 25, estimate P(fewer than 7) with n 14
rse
approximation is not suitable.
and
p 0.6 by using the normal distribution as an approximation to the binomial distribution; if np< 5 or nq<5, then state that the normal
Select the correct choice below and, if necessary, fill in the answer box to complete your
ou
choice
O A. P(fewer than 7)=
(Round to four decimal places as needed.)
ign
B. The normal approximation is not suitable.
dy
adel
atCr
Тext
Click to select and enter your answer(s) and then click Check Answer
hapt
Check Answer
Clear All
All parts showing
Tools fo
OK
10:30
3 ^#
12/3
e
Ot
Type here to search
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 3 images

Recommended textbooks for you

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

Elementary Statistics: Picturing the World (7th E…
Statistics
ISBN:
9780134683416
Author:
Ron Larson, Betsy Farber
Publisher:
PEARSON

The Basic Practice of Statistics
Statistics
ISBN:
9781319042578
Author:
David S. Moore, William I. Notz, Michael A. Fligner
Publisher:
W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:
9781319013387
Author:
David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:
W. H. Freeman