If w is a complex root of z7 - 1 = 0. .5 z 3 Show that w is a solution of 2 z z z z 1 = 0. i. Find a quadratic equation with real coefficients having a root www ii. 2т Зп 1 TT iii. Prove that cos 7 COS 7 COS 7 2
If w is a complex root of z7 - 1 = 0. .5 z 3 Show that w is a solution of 2 z z z z 1 = 0. i. Find a quadratic equation with real coefficients having a root www ii. 2т Зп 1 TT iii. Prove that cos 7 COS 7 COS 7 2
Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter11: Topics From Analytic Geometry
Section: Chapter Questions
Problem 33RE
Related questions
Question
Part ii only please!
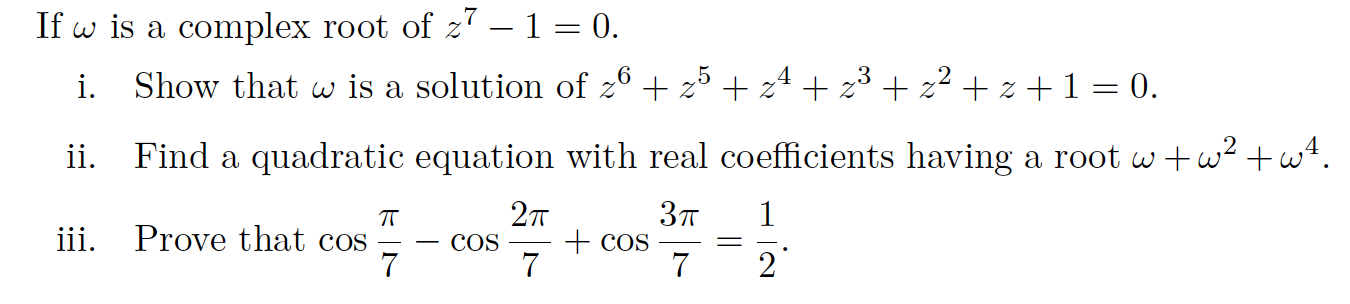
Transcribed Image Text:If w is a complex root of z7 - 1 = 0.
.5
z
3
Show that w is a solution of 2 z
z
z
z 1 = 0.
i.
Find a quadratic equation with real coefficients having a root www
ii.
2т
Зп
1
TT
iii. Prove that cos
7
COS
7
COS
7
2
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 7 steps with 7 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Elements Of Modern Algebra
Algebra
ISBN:
9781285463230
Author:
Gilbert, Linda, Jimmie
Publisher:
Cengage Learning,

Algebra for College Students
Algebra
ISBN:
9781285195780
Author:
Jerome E. Kaufmann, Karen L. Schwitters
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Elements Of Modern Algebra
Algebra
ISBN:
9781285463230
Author:
Gilbert, Linda, Jimmie
Publisher:
Cengage Learning,

Algebra for College Students
Algebra
ISBN:
9781285195780
Author:
Jerome E. Kaufmann, Karen L. Schwitters
Publisher:
Cengage Learning