Let G (Z/18Z, +) be a cyclic group of order 18. (1) Find a subgroup H of G with |H= 3 (2) What are the elements of G/H? (3) Find a familiar group that is isomorphic to G/H.
Let G (Z/18Z, +) be a cyclic group of order 18. (1) Find a subgroup H of G with |H= 3 (2) What are the elements of G/H? (3) Find a familiar group that is isomorphic to G/H.
Elements Of Modern Algebra
8th Edition
ISBN:9781285463230
Author:Gilbert, Linda, Jimmie
Publisher:Gilbert, Linda, Jimmie
Chapter4: More On Groups
Section4.4: Cosets Of A Subgroup
Problem 11E: Let be a group of order 24. If is a subgroup of , what are all the possible orders of ?
Related questions
Question
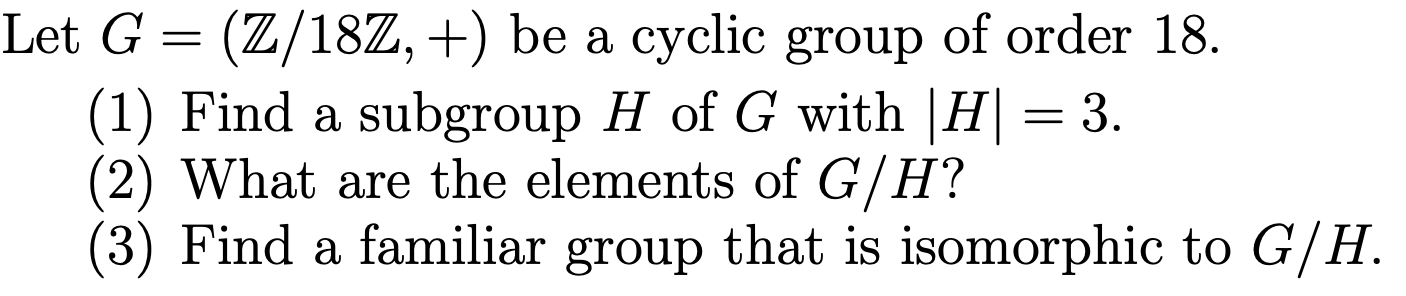
Transcribed Image Text:Let G
(Z/18Z, +) be a cyclic group of order 18.
(1) Find a subgroup H of G with |H= 3
(2) What are the elements of G/H?
(3) Find a familiar group that is isomorphic to G/H.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 5 steps with 3 images

Recommended textbooks for you

Elements Of Modern Algebra
Algebra
ISBN:
9781285463230
Author:
Gilbert, Linda, Jimmie
Publisher:
Cengage Learning,

Elements Of Modern Algebra
Algebra
ISBN:
9781285463230
Author:
Gilbert, Linda, Jimmie
Publisher:
Cengage Learning,