mass m is fixed to Pendulum A simple pendulum consisting of a point 1. the end of a massless rod (length /), whose other end is pivoted from the ceiling to let it swing freely in a vertical plane, specified by its angle o from the equilibrium position. (a) Prove that the pendulum's potential energy (measured from the equilibrium level) is as shown below. The pendulum's position can be U ()mgl (1 - cos ) (b) Write down the total energy E as a function of and o. Show that by differentiating your expression for E with respect to t you can get the equation of motion for ¢ and that the equation of motion is just the familiar T moment of inertia, and a is the angular acceleration ). (c) Assuming that the angle remains small throughout the motion, show that the motion is periodic with period Ia (where T is the torque, I is the - 2т V1/9. Tо m 1 (d)To get the pendulum's period good for large oscillations as well as small, the following method: Use the above PE, find we can use do as a function of d. Next use 11 dt in the form t do/o, to write the time for the pendulum to travel from ø = 0 to its maximum value (the amplitude) . Now show that du -Ф do 2 То - T TO 1 VI-u2I-A2u2 sin (d/2) sin2 (ø/2) 0 is the period for small oscillation given above and A = sin(P/2). These inte- where To grals cannot be evaluated in terms of elementary functions. However, the second integral is a standard integral called the complete elliptic integral of the first kind, sometimes de- noted K(A2), whose values are tabulated and are known to computer software such as Mathematica, which calls it EllipticK (A2)].
mass m is fixed to Pendulum A simple pendulum consisting of a point 1. the end of a massless rod (length /), whose other end is pivoted from the ceiling to let it swing freely in a vertical plane, specified by its angle o from the equilibrium position. (a) Prove that the pendulum's potential energy (measured from the equilibrium level) is as shown below. The pendulum's position can be U ()mgl (1 - cos ) (b) Write down the total energy E as a function of and o. Show that by differentiating your expression for E with respect to t you can get the equation of motion for ¢ and that the equation of motion is just the familiar T moment of inertia, and a is the angular acceleration ). (c) Assuming that the angle remains small throughout the motion, show that the motion is periodic with period Ia (where T is the torque, I is the - 2т V1/9. Tо m 1 (d)To get the pendulum's period good for large oscillations as well as small, the following method: Use the above PE, find we can use do as a function of d. Next use 11 dt in the form t do/o, to write the time for the pendulum to travel from ø = 0 to its maximum value (the amplitude) . Now show that du -Ф do 2 То - T TO 1 VI-u2I-A2u2 sin (d/2) sin2 (ø/2) 0 is the period for small oscillation given above and A = sin(P/2). These inte- where To grals cannot be evaluated in terms of elementary functions. However, the second integral is a standard integral called the complete elliptic integral of the first kind, sometimes de- noted K(A2), whose values are tabulated and are known to computer software such as Mathematica, which calls it EllipticK (A2)].
Related questions
Question
can you do part d please
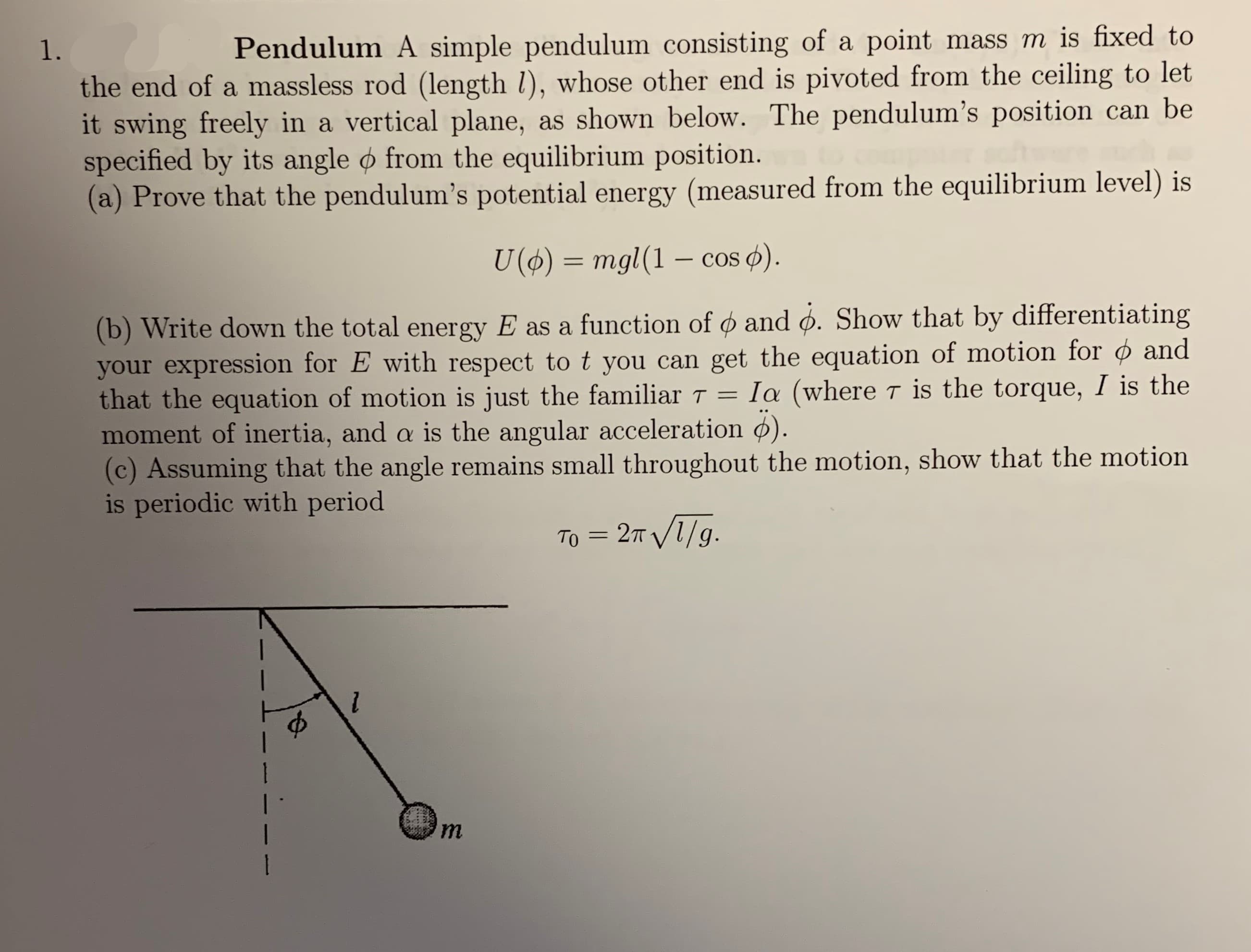
Transcribed Image Text:mass m is fixed to
Pendulum A simple pendulum consisting of a point
1.
the end of a massless rod (length /), whose other end is pivoted from the ceiling to let
it swing freely in a vertical plane,
specified by its angle o from the equilibrium position.
(a) Prove that the pendulum's potential energy (measured from the equilibrium level) is
as shown below. The pendulum's position can be
U ()mgl (1 - cos )
(b) Write down the total energy E as a function of and o. Show that by differentiating
your expression for E with respect to t you can get the equation of motion for ¢ and
that the equation of motion is just the familiar T
moment of inertia, and a is the angular acceleration ).
(c) Assuming that the angle remains small throughout the motion, show that the motion
is periodic with period
Ia (where T is the torque, I is the
- 2т V1/9.
Tо
m
1
![(d)To get the pendulum's period good for large oscillations as well as small,
the following method: Use the above PE, find
we can use
do
as a function of d. Next use
11
dt
in the form t
do/o, to write the time for the pendulum to travel from ø = 0 to its
maximum value (the amplitude) . Now show that
du
-Ф
do
2
То -
T TO
1
VI-u2I-A2u2
sin (d/2) sin2 (ø/2)
0
is the period for small oscillation given above and A = sin(P/2). These inte-
where To
grals cannot be evaluated in terms of elementary functions. However, the second integral
is a standard integral called the complete elliptic integral of the first kind, sometimes de-
noted K(A2), whose values are tabulated and are known to computer software such as
Mathematica, which calls it EllipticK (A2)].](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Ffa4426dc-92c3-4ac7-bd5a-9ba1dd10b9af%2F170c46b0-de22-4654-ba6c-b600e3729575%2F3ni8q5i.jpeg&w=3840&q=75)
Transcribed Image Text:(d)To get the pendulum's period good for large oscillations as well as small,
the following method: Use the above PE, find
we can use
do
as a function of d. Next use
11
dt
in the form t
do/o, to write the time for the pendulum to travel from ø = 0 to its
maximum value (the amplitude) . Now show that
du
-Ф
do
2
То -
T TO
1
VI-u2I-A2u2
sin (d/2) sin2 (ø/2)
0
is the period for small oscillation given above and A = sin(P/2). These inte-
where To
grals cannot be evaluated in terms of elementary functions. However, the second integral
is a standard integral called the complete elliptic integral of the first kind, sometimes de-
noted K(A2), whose values are tabulated and are known to computer software such as
Mathematica, which calls it EllipticK (A2)].
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 6 steps with 6 images
