Question 10 The complex number B is given by B (1- t) + (2t)i, where t is real. II tan) (i) Show that IB = 1 + t2 and arg(B) 0 where t = t (ii) Write down the modulus and argument of one square root of B, and hence if z2 = B, write z in the form a + ib where a and b are real. (iii) Hence find the two square roots of -8+ 6i
[Lin WS - Question 10]
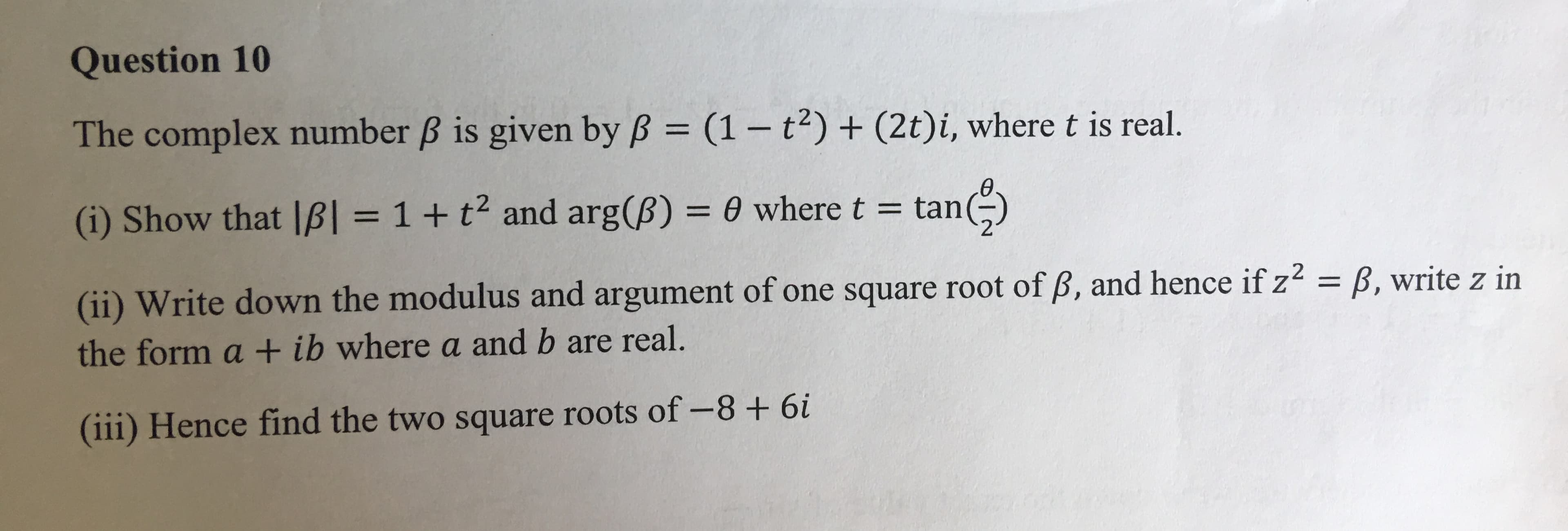
Hi, Question is Attached
Image Transcriptionclose
Question 10 The complex number B is given by B (1- t) + (2t)i, where t is real. II tan) (i) Show that IB = 1 + t2 and arg(B) 0 where t = t (ii) Write down the modulus and argument of one square root of B, and hence if z2 = B, write z in the form a + ib where a and b are real. (iii) Hence find the two square roots of -8+ 6i
Expert Answer
Related Advanced Math Q&A
Q: Exercise 7: Use the 8-e definition to prove: lim f(x) L lim f(c+ h) L. h- 0 Exercise 8: (a) Prove li...
A: It is given that
Q: Let A, B, C be three collinear points and let P be a point outside the line through A, B, C. Using t...
A: Sketch the diagrams with the help of geometrical tools and the hint given in the question.
Q: Solve the given initial-value problem. y'' + 4y' + 5y = 35e-4x y(0)= -5, y'(0)= 1 y(x)= ____________...
A: From the given information the given differential equation is:
Q: Advanced Math Question
A: There are 5 functions given s(t) = t3, z(x) = 3x, m(x) = 12x6, f(x) = 3x + 1, g(x) = x2 Create the b...
Q: How do you solve?
A: To determine the number of advertisements in each category to secure the maximum exposure
Q: ntemporary Math Module 6: Graph Theory Mod 6 Quiz Graph Theory B 13 C 1 6 10 A 12 11 D to the graph ...
A: The repeated nearest neighbour algorithm apply as follow,Let we start from vertex A, then the unvisi...
Q: The altitudes of a triangle ABC intersect at a point H. Let O, be the circumcenter of the A triangle...
A: Given ABC be a triangle, and H be the altitude that intersect to the triangle.Draw the circumcenter ...
Q: need help with this for History of Math Stilwell 8.7.2 dealing with projective geometry
A: Proof:
Q: A bumblebee is flying so that its position is given by~r(t) = cos(2t), cos(3t),sin(5t) for the oscul...
A: Before we start the problem let us get to know the formula first.
