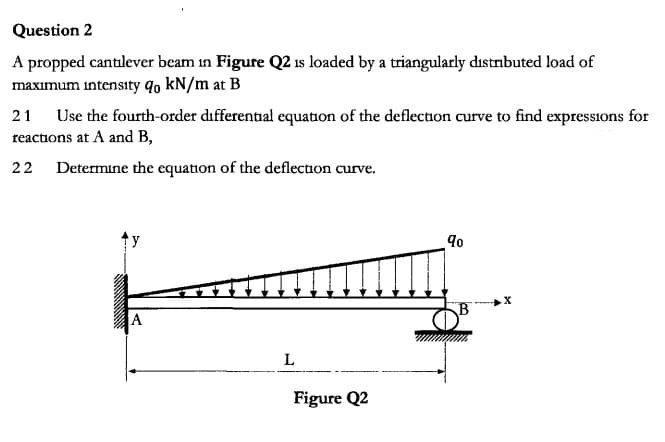
Question 2 A propped cantlever beam in Figure Q2 is loaded by a triangularly distrnbuted load of maximum intensity qo kN/m at B Use the fourth-order differental equation of the deflection curve to find expressions for reactions at A and B, 21 Determine the equation of the deflection curve. 22 A L Figure Q2
Question 2 A propped cantlever beam in Figure Q2 is loaded by a triangularly distrnbuted load of maximum intensity qo kN/m at B Use the fourth-order differental equation of the deflection curve to find expressions for reactions at A and B, 21 Determine the equation of the deflection curve. 22 A L Figure Q2
Mechanics of Materials (MindTap Course List)
9th Edition
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Barry J. Goodno, James M. Gere
Chapter9: Deflections Of Beams
Section: Chapter Questions
Problem 9.4.8P: Derive the equation of the deflection curve for beam AB with sliding support at A and roller at B*...
Related questions
Question
Transcribed Image Text:Question 2
A propped cantlever beam in Figure Q2 is loaded by a triangularly distrnbuted load of
maximum intensity qo kN/m at B
Use the fourth-order differental equation of the deflection curve to find expressions for
reactions at A and B,
21
Determine the equation of the deflection curve.
22
A
L
Figure Q2
Expert Solution
Trending now
This is a popular solution!
Step by step
Solved in 10 steps with 10 images

Recommended textbooks for you

Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:
9781337093347
Author:
Barry J. Goodno, James M. Gere
Publisher:
Cengage Learning

Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:
9781337093347
Author:
Barry J. Goodno, James M. Gere
Publisher:
Cengage Learning