ral matix expresse particule EXERCISES 2.8 A is TON Exercises 1-4 display sets in R2. Assume the sets include the bounding lines. In each case, give a specific reason why the set H is not a subspace of R2. (For instance, find two vectors in H whose sura is not in H, or find a vector in H with a scalar multiple that is not i H. Draw a picture.) 7. Let vi equation f A have р3D 1. а. Но b. Hо с. Is 8. Let v 14 9 2. 2, and 5 ect linear 9. With 10. With in Nu In Exercis subspace eeded t , because e relation } is als 11. А 3D 3. 12. А - 13. For non 4. 14. For non A.T nstance can Determi Justify e 15. Deter- 2 and w = 5. Let vi -5 3 V2 8 -5 mine if w is in the subspace of R generated by vi and v2. 17.
ral matix expresse particule EXERCISES 2.8 A is TON Exercises 1-4 display sets in R2. Assume the sets include the bounding lines. In each case, give a specific reason why the set H is not a subspace of R2. (For instance, find two vectors in H whose sura is not in H, or find a vector in H with a scalar multiple that is not i H. Draw a picture.) 7. Let vi equation f A have р3D 1. а. Но b. Hо с. Is 8. Let v 14 9 2. 2, and 5 ect linear 9. With 10. With in Nu In Exercis subspace eeded t , because e relation } is als 11. А 3D 3. 12. А - 13. For non 4. 14. For non A.T nstance can Determi Justify e 15. Deter- 2 and w = 5. Let vi -5 3 V2 8 -5 mine if w is in the subspace of R generated by vi and v2. 17.
Linear Algebra: A Modern Introduction
4th Edition
ISBN:9781285463247
Author:David Poole
Publisher:David Poole
Chapter6: Vector Spaces
Section: Chapter Questions
Problem 5RQ
Related questions
Question
I don't understand how to do problems 2,3,4.
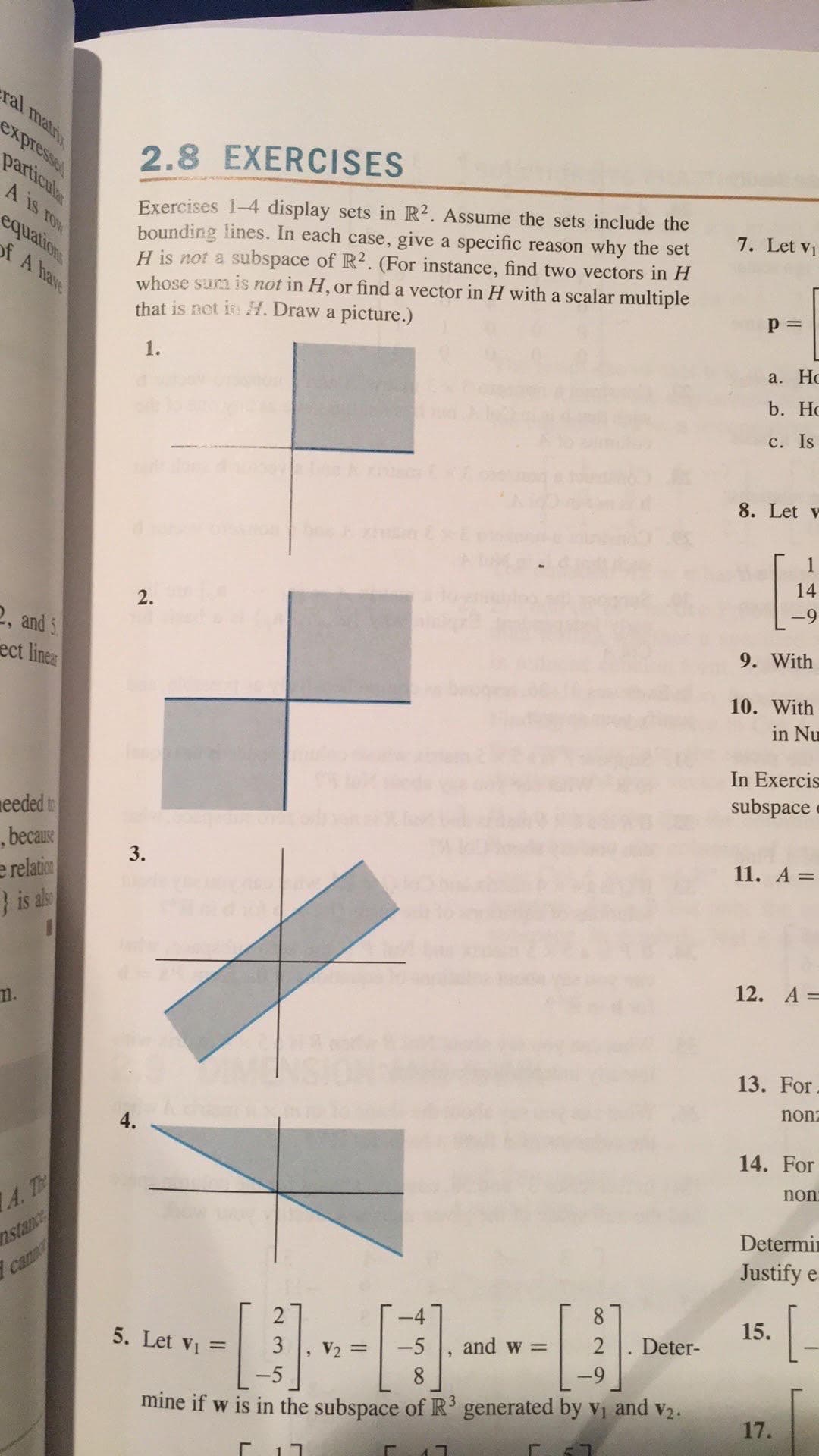
Transcribed Image Text:ral matix
expresse
particule
EXERCISES
2.8
A is TON
Exercises 1-4 display sets in R2. Assume the sets include the
bounding lines. In each case, give a specific reason why the set
H is not a subspace of R2. (For instance, find two vectors in H
whose sura is not in H, or find a vector in H with a scalar multiple
that is not i H. Draw a picture.)
7. Let vi
equation
f A have
р3D
1.
а. Но
b. Hо
с. Is
8. Let v
14
9
2.
2, and 5
ect linear
9. With
10. With
in Nu
In Exercis
subspace
eeded t
, because
e relation
} is als
11. А 3D
3.
12. А -
13. For
non
4.
14. For
non
A.T
nstance
can
Determi
Justify e
15.
Deter-
2
and w =
5. Let vi
-5
3
V2
8
-5
mine if w is in the subspace of R generated by vi and v2.
17.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 3 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:
9781305658004
Author:
Ron Larson
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:
9781305658004
Author:
Ron Larson
Publisher:
Cengage Learning