The following series are geometric series or a sum of two geometric series. Determine whether each series converges or not. For the series which converge, enter the sum of the series. For the series which diverges enter "DIV" (without quotes). 00 6" (a) E 5" n=1 1 (b) 3" n=2 00 3" 82n+1 n=0
The following series are geometric series or a sum of two geometric series. Determine whether each series converges or not. For the series which converge, enter the sum of the series. For the series which diverges enter "DIV" (without quotes). 00 6" (a) E 5" n=1 1 (b) 3" n=2 00 3" 82n+1 n=0
Chapter9: Sequences, Probability And Counting Theory
Section9.4: Series And Their Notations
Problem 10TI: Determine whether the sum of the infinite series is defined. 24+(12)+6+(3)+
Related questions
Question
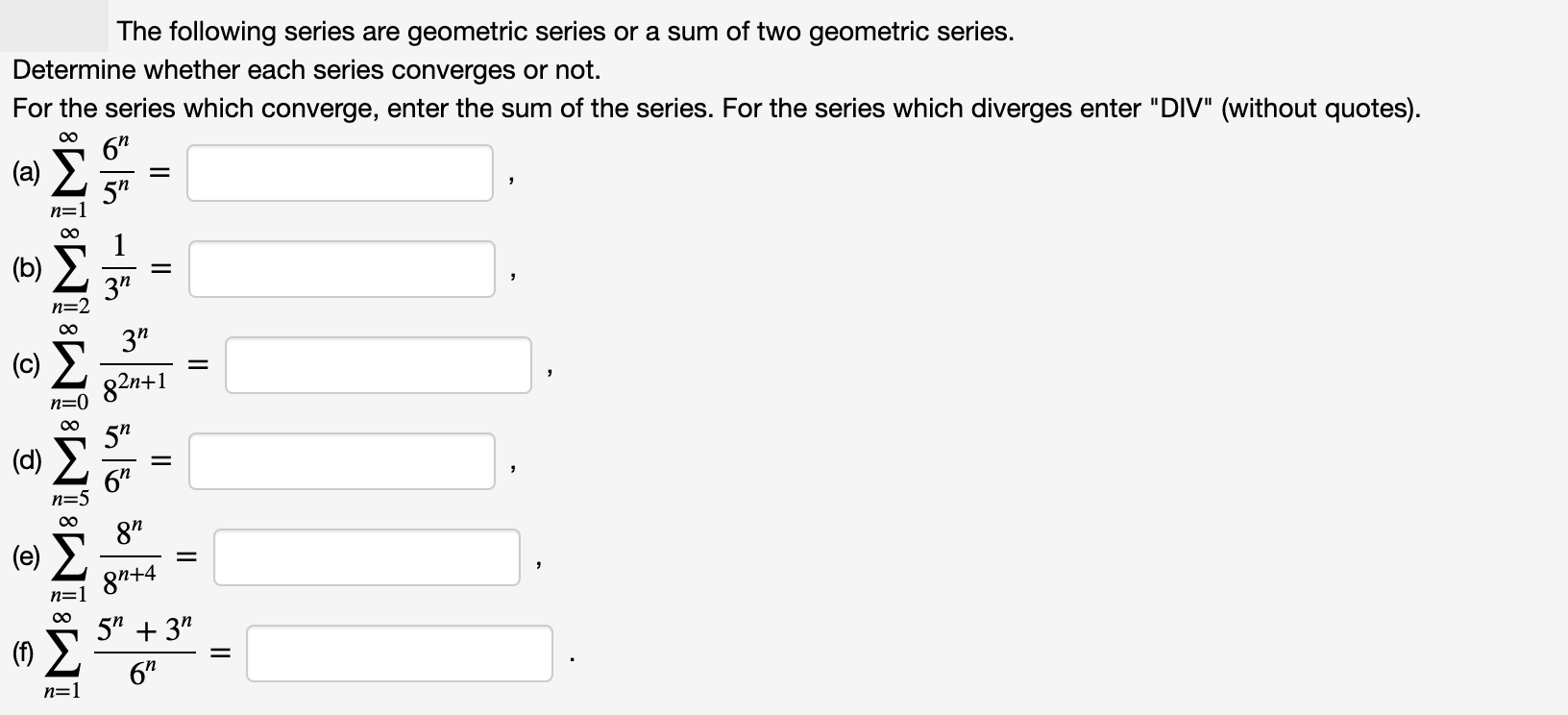
Transcribed Image Text:The following series are geometric series or a sum of two geometric series.
Determine whether each series converges or not.
For the series which converge, enter the sum of the series. For the series which diverges enter "DIV" (without quotes).
00
6"
(a) E
5"
n=1
1
(b)
3"
n=2
00
3"
82n+1
n=0
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 5 steps with 4 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Recommended textbooks for you


Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage


Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage