The per capita consumption of commercially produced fresh vegetables in a certain country from 1980 through 2000 was as shown in the accompanying table. Per capita consumption of fresh vegetables in a certain country Vegetable consumption, V (pounds per person) Year 1980 147.1 1985 157 1990 167.1 1995 176.1 200.7 2000 (a) Find the function of the quadratic model that gives the per capita consumption of fresh vegetables in pounds per person, where t is the number of years since 1980, with data from 0 sts 20. Examine the equation graphed on a scatter plot of the data (Round all numerical values to three decimal places.) V(t) (b) Do you believe that the equation in part (a) is a good fit? OThe model does not appear to be a good fit. OThe model appears to be a good fit. OThis cannot be determined. (c) The per capita consumption in 2001 had not yet been tabulated when the data in the table were published. What does the quadratic model give as the per capita consumption in 2001? (Round your answer to one decimal place.) 190 X pounds per person (d) According to your model, in what year will consumption exceed 225 pounds per person
The per capita consumption of commercially produced fresh vegetables in a certain country from 1980 through 2000 was as shown in the accompanying table. Per capita consumption of fresh vegetables in a certain country Vegetable consumption, V (pounds per person) Year 1980 147.1 1985 157 1990 167.1 1995 176.1 200.7 2000 (a) Find the function of the quadratic model that gives the per capita consumption of fresh vegetables in pounds per person, where t is the number of years since 1980, with data from 0 sts 20. Examine the equation graphed on a scatter plot of the data (Round all numerical values to three decimal places.) V(t) (b) Do you believe that the equation in part (a) is a good fit? OThe model does not appear to be a good fit. OThe model appears to be a good fit. OThis cannot be determined. (c) The per capita consumption in 2001 had not yet been tabulated when the data in the table were published. What does the quadratic model give as the per capita consumption in 2001? (Round your answer to one decimal place.) 190 X pounds per person (d) According to your model, in what year will consumption exceed 225 pounds per person
Functions and Change: A Modeling Approach to College Algebra (MindTap Course List)
6th Edition
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Bruce Crauder, Benny Evans, Alan Noell
Chapter5: A Survey Of Other Common Functions
Section5.6: Higher-degree Polynomials And Rational Functions
Problem 3E: Traffic Accidents The following table shows the cost C of traffic accidents. in cents per...
Related questions
Concept explainers
Contingency Table
A contingency table can be defined as the visual representation of the relationship between two or more categorical variables that can be evaluated and registered. It is a categorical version of the scatterplot, which is used to investigate the linear relationship between two variables. A contingency table is indeed a type of frequency distribution table that displays two variables at the same time.
Binomial Distribution
Binomial is an algebraic expression of the sum or the difference of two terms. Before knowing about binomial distribution, we must know about the binomial theorem.
Topic Video
Question
i am having trouble with this one
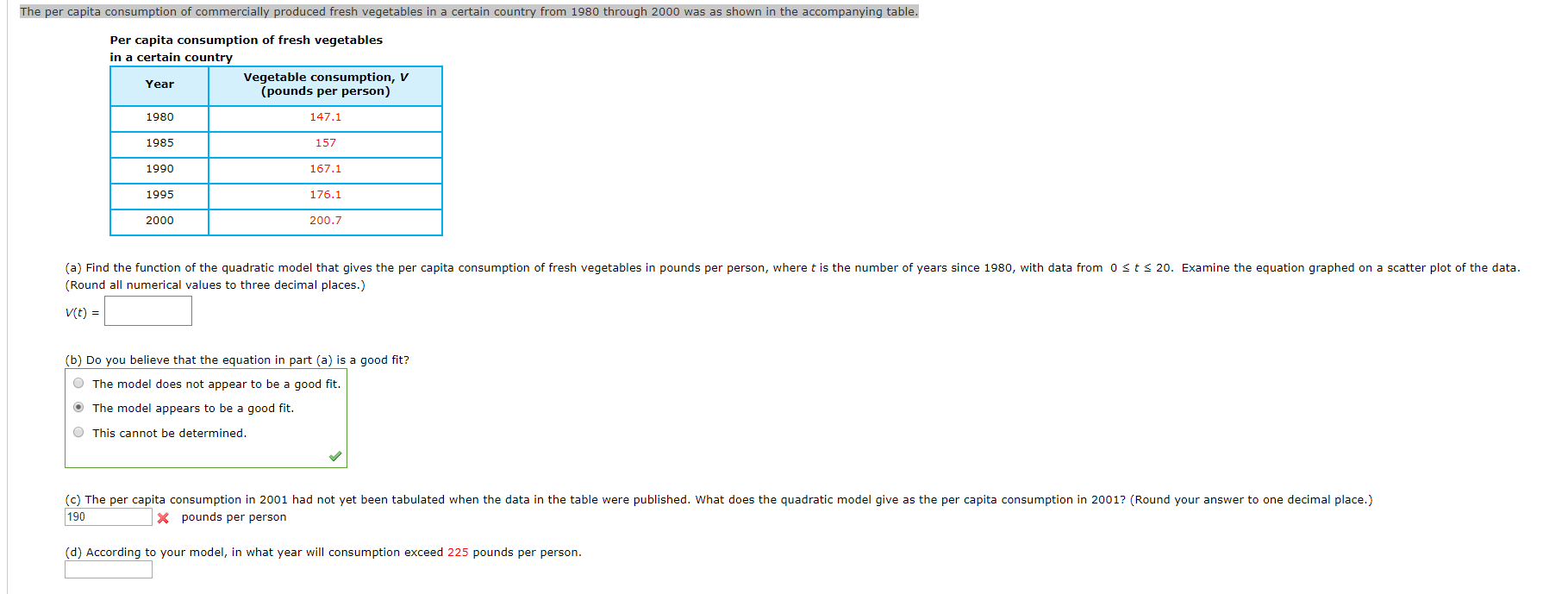
Transcribed Image Text:The per capita consumption of commercially produced fresh vegetables in a certain country from 1980 through 2000 was as shown in the accompanying table.
Per capita consumption of fresh vegetables
in a certain country
Vegetable consumption, V
(pounds per person)
Year
1980
147.1
1985
157
1990
167.1
1995
176.1
200.7
2000
(a) Find the function of the quadratic model that gives the per capita consumption of fresh vegetables in pounds per person, where t is the number of years since 1980, with data from 0 sts 20. Examine the equation graphed on a scatter plot of the data
(Round all numerical values to three decimal places.)
V(t)
(b) Do you believe that the equation in part (a) is a good fit?
OThe model does not appear to be a good fit.
OThe model appears to be a good fit.
OThis cannot be determined.
(c) The per capita consumption in 2001 had not yet been tabulated when the data in the table were published. What does the quadratic model give as the per capita consumption in 2001? (Round your answer to one decimal place.)
190
X pounds per person
(d) According to your model, in what year will consumption exceed 225 pounds per person
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 4 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Recommended textbooks for you

Functions and Change: A Modeling Approach to Coll…
Algebra
ISBN:
9781337111348
Author:
Bruce Crauder, Benny Evans, Alan Noell
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Functions and Change: A Modeling Approach to Coll…
Algebra
ISBN:
9781337111348
Author:
Bruce Crauder, Benny Evans, Alan Noell
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage