Use a change of variables to evaluate the following integral cos x) sin x dx 5 -(cos 'x-5 cos x-c (cos 7x-5 cos x- cos x) sinx dx 5 (Use C as the arbitrary constant.)
Use a change of variables to evaluate the following integral cos x) sin x dx 5 -(cos 'x-5 cos x-c (cos 7x-5 cos x- cos x) sinx dx 5 (Use C as the arbitrary constant.)
Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter7: Analytic Trigonometry
Section7.4: Multiple-angle Formulas
Problem 54E
Related questions
Question
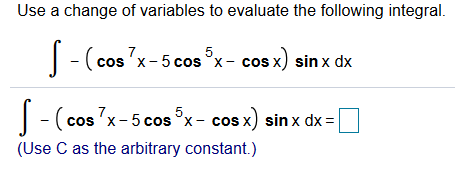
Transcribed Image Text:Use a change of variables to evaluate the following integral
cos x) sin x dx
5
-(cos 'x-5 cos x-c
(cos 7x-5 cos x- cos x) sinx dx
5
(Use C as the arbitrary constant.)
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 6 steps with 6 images

Recommended textbooks for you

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage