V4. Given: Chord AB = chord CD %3D Prove: AP = CP; BP = DP %3D %3D Excerases 5.7 # 28.1114 4 pq. 121 * Fextbook Crahements Rreanons 1. Crche O won diarneber 1. Buven chard cD nób a diameber 2. Boance from 2. Pel. & dianeber to ArB =8 Czero 3. Draw OE L CD 3. Exactiy 1 1 can be dramen to a Vane from a A. atorde Bhe Vive. of 11 Can be 4. DE >Ø 4 The whdee > ary ts parts 5. Theorem 38 5. AB> CD Gven: Chard AB = chard Cb Stabements Reagens Prong: AD cB %3D 1. Gven 1. Chad AB Chard co havn2. Is Bhe some carcle, equal chards Mbtend equal arcs. 8 the whole is = Phe Sum of ah part 2. A 3. ÁB- AD+pE 4. AD +PB - CB +e 5. ÁD = CB Stabements 1. Cwcle, dianebey AB b CD chad F ; AB I co, EF I| AB 4 Subostitutren 5. Sulbractren Rearens 1. Gvey 2. 2. CD 1EF 3. A drometer 3. Co binects EP Rosens Batements 1. Gwen 1. Crdle O, deaeter AB A,
V4. Given: Chord AB = chord CD %3D Prove: AP = CP; BP = DP %3D %3D Excerases 5.7 # 28.1114 4 pq. 121 * Fextbook Crahements Rreanons 1. Crche O won diarneber 1. Buven chard cD nób a diameber 2. Boance from 2. Pel. & dianeber to ArB =8 Czero 3. Draw OE L CD 3. Exactiy 1 1 can be dramen to a Vane from a A. atorde Bhe Vive. of 11 Can be 4. DE >Ø 4 The whdee > ary ts parts 5. Theorem 38 5. AB> CD Gven: Chard AB = chard Cb Stabements Reagens Prong: AD cB %3D 1. Gven 1. Chad AB Chard co havn2. Is Bhe some carcle, equal chards Mbtend equal arcs. 8 the whole is = Phe Sum of ah part 2. A 3. ÁB- AD+pE 4. AD +PB - CB +e 5. ÁD = CB Stabements 1. Cwcle, dianebey AB b CD chad F ; AB I co, EF I| AB 4 Subostitutren 5. Sulbractren Rearens 1. Gvey 2. 2. CD 1EF 3. A drometer 3. Co binects EP Rosens Batements 1. Gwen 1. Crdle O, deaeter AB A,
Chapter5: Exponential And Logarithmic Functions
Section5.5: Exponential And Logarithmic Models
Problem 6ECP: Find the intensities of earthquakes whose magnitudes are (a) R=6.0 and (b) R=7.9.
Related questions
Topic Video
Question
About geometry
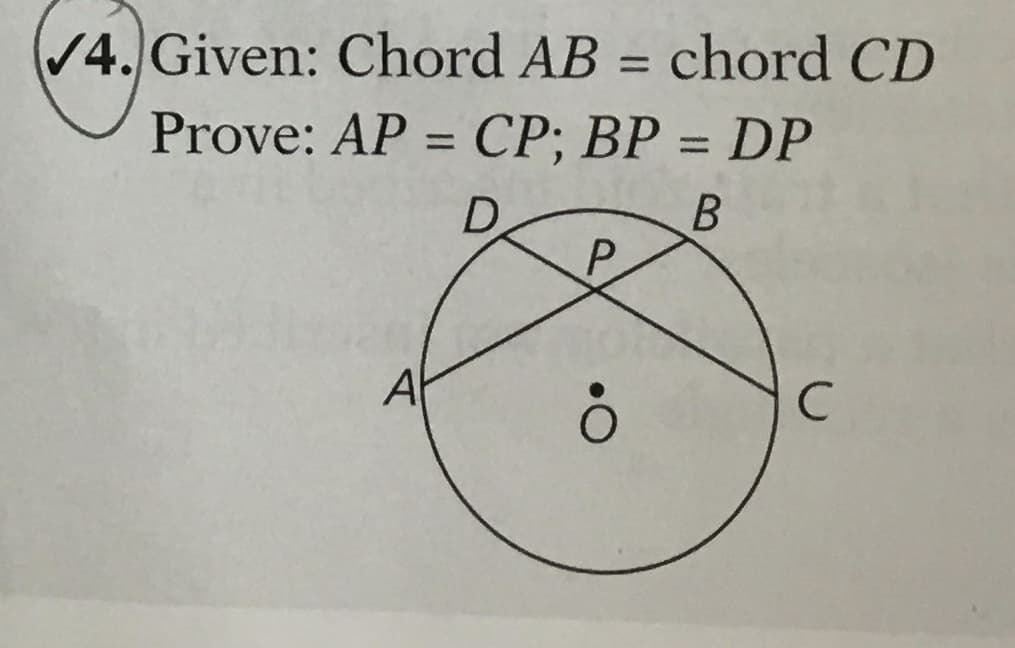
Transcribed Image Text:V4. Given: Chord AB = chord CD
%3D
Prove: AP = CP; BP = DP
%3D
%3D

Transcribed Image Text:Excerases 5.7 # 28.1114
4 pq. 121 * Fextbook
Crahements
Rreanons
1. Crche O won diarneber 1. Buven
chard cD nób a
diameber
2. Boance from
2. Pel. & dianeber
to
ArB =8 Czero
3. Draw OE L CD
3. Exactiy 1 1 can be
dramen to a Vane from a
A. atorde Bhe Vive.
of
11 Can be
4. DE >Ø
4 The whdee > ary
ts parts
5. Theorem 38
5. AB> CD
Gven: Chard AB = chard Cb
Stabements
Reagens
Prong: AD cB
%3D
1. Gven
1. Chad AB Chard co
havn2. Is Bhe some carcle, equal chards
Mbtend equal arcs.
8 the whole is = Phe Sum of ah part
2. A
3. ÁB- AD+pE
4. AD +PB - CB +e
5. ÁD = CB
Stabements
1. Cwcle, dianebey AB b CD
chad F ; AB I co, EF I| AB
4 Subostitutren
5. Sulbractren
Rearens
1. Gvey
2.
2. CD 1EF
3. A drometer
3. Co binects EP
Rosens
Batements
1. Gwen
1. Crdle O, deaeter AB
A,
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 1 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Recommended textbooks for you


Glencoe Algebra 1, Student Edition, 9780079039897…
Algebra
ISBN:
9780079039897
Author:
Carter
Publisher:
McGraw Hill

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,


Glencoe Algebra 1, Student Edition, 9780079039897…
Algebra
ISBN:
9780079039897
Author:
Carter
Publisher:
McGraw Hill

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,