With an initial approximation of xo = 3, use Newton's Method to approximate /7, correct to at least three significant digits. Show the approximation generated by each iteration and (when possible) its absolute relative approximate error. How many iterations were needed? с
With an initial approximation of xo = 3, use Newton's Method to approximate /7, correct to at least three significant digits. Show the approximation generated by each iteration and (when possible) its absolute relative approximate error. How many iterations were needed? с
Functions and Change: A Modeling Approach to College Algebra (MindTap Course List)
6th Edition
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Bruce Crauder, Benny Evans, Alan Noell
Chapter2: Graphical And Tabular Analysis
Section2.1: Tables And Trends
Problem 1TU: If a coffee filter is dropped, its velocity after t seconds is given by v(t)=4(10.0003t) feet per...
Related questions
Question
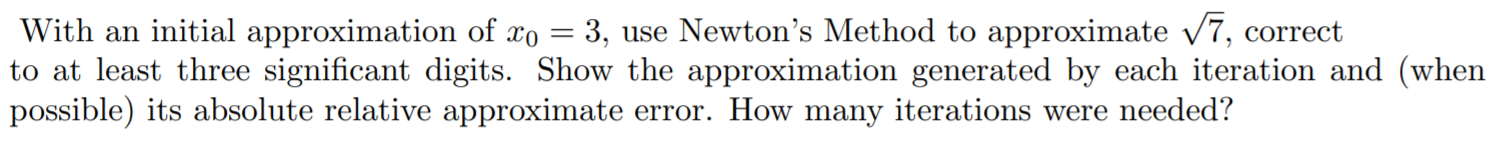
Transcribed Image Text:With an initial approximation of xo = 3, use Newton's Method to approximate /7, correct
to at least three significant digits. Show the approximation generated by each iteration and (when
possible) its absolute relative approximate error. How many iterations were needed?
с
Expert Solution
Step by step
Solved in 9 steps with 8 images

Recommended textbooks for you

Functions and Change: A Modeling Approach to Coll…
Algebra
ISBN:
9781337111348
Author:
Bruce Crauder, Benny Evans, Alan Noell
Publisher:
Cengage Learning

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning


Functions and Change: A Modeling Approach to Coll…
Algebra
ISBN:
9781337111348
Author:
Bruce Crauder, Benny Evans, Alan Noell
Publisher:
Cengage Learning

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning


Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage