y* - 4y2 =x4 -9x2 21. Find the slopes of the devil's curve at the four indicated points. y4- 4y2 x4-9x2 (3,2) (3,2) х -3 3 (3,-2) (-3, 2) The slope of the devil's curve at the point (-3, 2) is (Simplify your answer.) The slope of the devil's curve at the point (-3, -2) is (Simplify your answer.) The slope of the devil's curve at the point (3, 2) is (Simplify your answer.) The slope of the devil's curve at the point (3, - 2) is . (Simplify your answer.)
y* - 4y2 =x4 -9x2 21. Find the slopes of the devil's curve at the four indicated points. y4- 4y2 x4-9x2 (3,2) (3,2) х -3 3 (3,-2) (-3, 2) The slope of the devil's curve at the point (-3, 2) is (Simplify your answer.) The slope of the devil's curve at the point (-3, -2) is (Simplify your answer.) The slope of the devil's curve at the point (3, 2) is (Simplify your answer.) The slope of the devil's curve at the point (3, - 2) is . (Simplify your answer.)
Algebra and Trigonometry (MindTap Course List)
4th Edition
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:James Stewart, Lothar Redlin, Saleem Watson
Chapter1: Equations And Graphs
Section1.CR: Chapter Review
Problem 6CC
Related questions
Concept explainers
Equations and Inequations
Equations and inequalities describe the relationship between two mathematical expressions.
Linear Functions
A linear function can just be a constant, or it can be the constant multiplied with the variable like x or y. If the variables are of the form, x2, x1/2 or y2 it is not linear. The exponent over the variables should always be 1.
Question
Can you help me with this problem step by step?
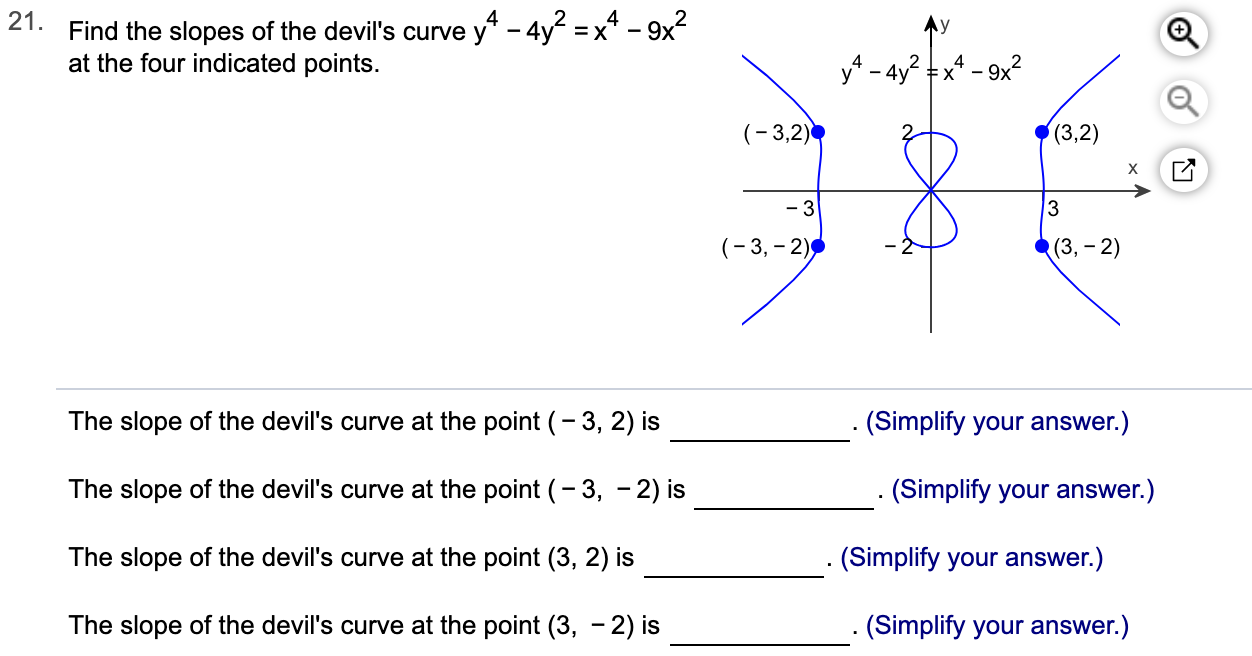
Transcribed Image Text:y* - 4y2 =x4 -9x2
21. Find the slopes of the devil's curve
at the four indicated points.
y4- 4y2 x4-9x2
(3,2)
(3,2)
х
-3
3
(3,-2)
(-3, 2)
The slope of the devil's curve at the point (-3, 2) is
(Simplify your answer.)
The slope of the devil's curve at the point (-3, -2) is
(Simplify your answer.)
The slope of the devil's curve at the point (3, 2) is
(Simplify your answer.)
The slope of the devil's curve at the point (3, - 2) is
. (Simplify your answer.)
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 7 steps with 7 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Recommended textbooks for you

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:
9781305071742
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning

College Algebra
Algebra
ISBN:
9781305115545
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning

Holt Mcdougal Larson Pre-algebra: Student Edition…
Algebra
ISBN:
9780547587776
Author:
HOLT MCDOUGAL
Publisher:
HOLT MCDOUGAL

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:
9781305071742
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning

College Algebra
Algebra
ISBN:
9781305115545
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning

Holt Mcdougal Larson Pre-algebra: Student Edition…
Algebra
ISBN:
9780547587776
Author:
HOLT MCDOUGAL
Publisher:
HOLT MCDOUGAL

Elementary Algebra
Algebra
ISBN:
9780998625713
Author:
Lynn Marecek, MaryAnne Anthony-Smith
Publisher:
OpenStax - Rice University


Intermediate Algebra
Algebra
ISBN:
9781285195728
Author:
Jerome E. Kaufmann, Karen L. Schwitters
Publisher:
Cengage Learning