Chapter 1, Problem 28RE

The population of a certain species in a limited environment with initial population 100 and carrying capacity 1000 is

$P(t)=\frac{100,000}{100+900e^{-t}}$

where t is measured in years.

(a) Graph this function and estimated how long it takes for the population to reach 900.

(b) Find the inverse of this function and explain its meaning.

(c) Use the inverse function to find the time required for the population to reach 900. Compare with the result of part (a).

To determine

To estimate: The time taken in which the population reaches 900 with the help of graph of the given equation.

Answer to Problem 28RE

Solution:

The time taken in which the population to reach 900 is approximately 4.4 years.

Explanation of Solution

Given:

The initial population in an limited environment is 100 with the carrying capacity 1000.

Also the population at any instant of time t is, $P\left(t\right)=\frac{100,000}{100+900e^{-t}}$.

Graph:

Use online graph calculator and draw the graph of the function $P\left(t\right)=\frac{100,000}{100+900e^{-t}}$ when $P\left(t\right)=900$.

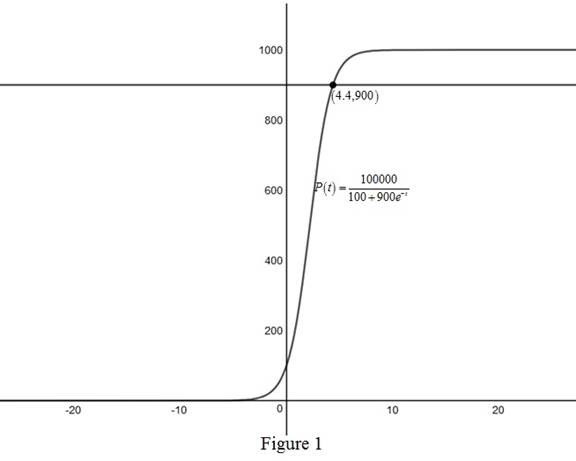
From Figure1,obtain that point of intersection of the graph of $P\left(t\right)=\frac{100,000}{100+900e^{-t}}$ and the line $y=900$ is $\left(4.4,900\right)$.

Therefore, time taken by the population to reach 900 is approximately 4.4 years.

To determine

To find: The inverse of the given function and to explain its meaning.

Answer to Problem 28RE

Solution:

The inverse of the function is $t=\ln \left[\frac{9P}{1000-P}\right]$ and the meaning of this inverse function is the time taken in which the population to reach P.

Explanation of Solution

Calculation:

Let $P\left(t\right)=P$.

$\begin{array}{c}P=\frac{100,000}{100+900e^{-t}}\\ 100+900e^{-t}=\frac{100,000}{P}\\ 900e^{-t}=\frac{100,000}{P}-100\\ e^{-t}=\frac{100.000}{900P}-\frac{100}{900}\end{array}$

Again solve the above equation,

$\begin{array}{c}{e}^{-t}=\frac{1000}{9P}-\frac{1}{9}\\ =\frac{1000}{9P}-\frac{P}{9P}\\ \frac{1}{e^t}=\frac{1000-P}{9P}\end{array}$

Take reciprocal on both sides,

$e^t=\frac{9P}{1000-P}$

Take natural logarithm on both sides,

$\ln e^t=\ln \left(\frac{9P}{1000-P}\right)$

Since $\ln e^t=t$,

Therefore, $t=\ln \left[\frac{9P}{1000-P}\right]$.

Where t is the inverse of the function and t denotes the time taken by the population to reach P.

To determine

To find: The time required by the population to reach 900 by using the inverse function.

Answer to Problem 28RE

Solution:

The time required for the population to reach 900 by using the inverse function is approximately 4.39 years.

Explanation of Solution

Calculation:

From part(b), the inverse of the function is $t=\ln \left[\frac{9P}{1000-P}\right]$.

Given that $P=900$.

Therefore, the inverse of the function is,

$\begin{array}{c}t=\ln \left[\frac{9\left(900\right)}{1000-900}\right]\\ =\ln \left[\frac{8100}{100}\right]\\ =\ln \left(81\right)\\ t\approx 4.39\end{array}$

Thus, the time required for the population to reach 900 by using the inverse function is approximately 4.39 years.

Compare this answer with the answer in part (b) and observe that the answers are approximately same.