Single Variable Calculus: Concepts and Contexts, Enhanced Edition

4th Edition

ISBN: 9781337687805

Author: James Stewart

Publisher: Cengage Learning

See similar textbooks

Concept explainers

Maximization

Have you ever seen a bridge in the shape of a parabola? Where is its maximum on the bridge? The maximum of that bridge is the highest point on that bridge. The process of finding the maximum of the bridge here is called the maximization.

Videos

Question

Chapter 1, Problem 34RE

To determine

Find parametric equations for the set of all points $P$ .

Expert Solution

Answer to Problem 34RE

$(a−acos2θ,2atanθ−asin2θ)$

Explanation of Solution

Given information:

Find parametric equations for the set of all points $P$ determined as shown in the figure such that $|OP|=|AB|$ .(This curve is called the cissoid of Diocles after the Greek scholar Diocles, who introduced the cissode as a graphical method for constructing the edge of a cube whose volume is twice that of a given cube.)

Single Variable Calculus: Concepts and Contexts, Enhanced Edition, Chapter 1, Problem 34RE , additional homework tip 1

Calculation:

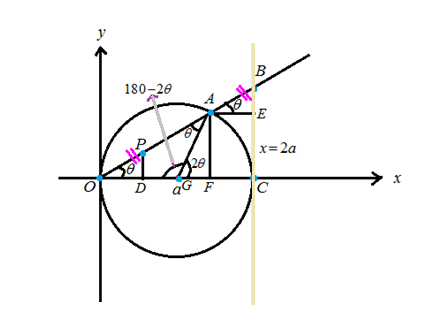
Consider the figure

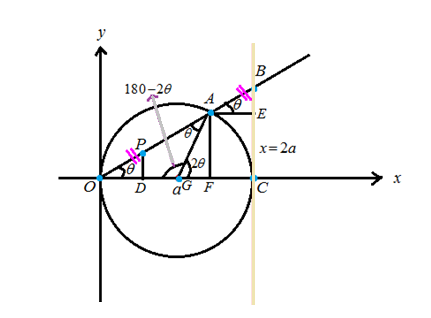
Single Variable Calculus: Concepts and Contexts, Enhanced Edition, Chapter 1, Problem 34RE , additional homework tip 2

Whereas $OG&GA$ are radii of the circle radius $a$ . So $OG&GA$ are congruent and so their opposite angles $OAG&AOG$ are congruent.

Hence $OAG=AOG=θ$ .

For the triangles $ABE&ODP$ , the sides $|OP|=|AB|$ and lines $BE‖PD$ (these lines are perpendicular to the $x−axis$ ) so the angles $BAE&POD$ are congruent.

Hence $BAE=POD=θ$ .

Consider the triangle $OBC$ to find the coordinates of the point $B$ .

Hence $OC=2a$ (diameter of the circle) and $BOC=θ$ , we have

$tanθ=BC2aBC=2atanθ$

The $x$ -coordinate of the point $B$ is $2a$ and the $y−$ coordinates is $2atanθ$ .

Hence the point $B=(2a,2atanθ)$ .

To find the point $A$ , we need to determine the distances $AF&OF$ .

In the triangle $OAG$ , sum of the angles are

$θ+θ+AGO=180°AGO=180°−2θ$

We know that

$AGO+AGF=180°180°−2θ+AGF=180°AGF=2θ$

Now consider the triangle $AGF,$ get

$sin2θ=AFAG=AFaAF=asin2θ$

And

$cos2θ=GFAG=GFaGF=acos2θ$

The $x−$ coordinate of the point $A$ is

$OG+GF=a+acos2θ$

The $y−$ coordinate of the point $A$ is $AF=asin2θ$ .

Hence, the point $A=(a+cos2θ,asin2θ)$ .

Find the distance $AE&BE:$

To get the distance $AE$ , we need to subtract the $x$ -coordinate of $A$ from the $x$ -coordinate of $B$ .

$AE=2a−(a+acos2θ)=a−acos2θ$

To get the distance $BE$ , we need to subtract the $y$ -coordinate of $A$ from the $y$ -coordinate of $B$ .

$BE=2atanθ−asin2θ$ .

The triangles $ABE&OPD$ are congruent whereas the sides $OP,AB$ are equal and the angles $BAE&POD$ are equal.

Hence, in these two triangles $ABE&OPD$ the corresponding sides $AE,OD$ are equal and $BE,PD$ are equal.

$AE=OD=a−acos2θ,BE=PD=2atanθ−asin2θ$

Hence, the required coordinates of the point $P$ is $(a−acos2θ,2atanθ−asin2θ)$ .

To determine

Use the geometric description of the curve to draw a rough of the curve by hand.

Expert Solution

Answer to Problem 34RE

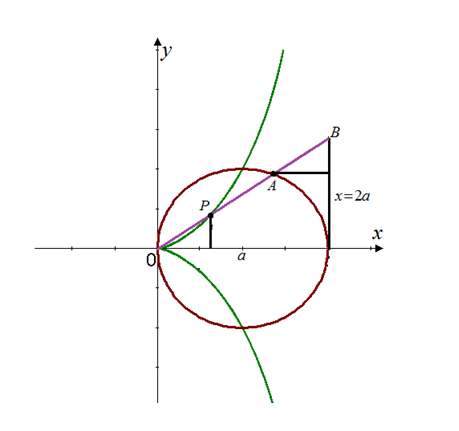
Single Variable Calculus: Concepts and Contexts, Enhanced Edition, Chapter 1, Problem 34RE , additional homework tip 3

Explanation of Solution

Given information:

Use the geometric description of the curve to draw a rough of the curve by hand. Check your work by using the parametric equations to graph the curve.

Single Variable Calculus: Concepts and Contexts, Enhanced Edition, Chapter 1, Problem 34RE , additional homework tip 4

Calculation:

Draw the curve represented by the parametric equations

$x(θ)=a−acos2θ,y(θ)=2atanθ−asin2θ$ .

This curve is known as cissoids of Diocles.

The graph of the curve is shown below:

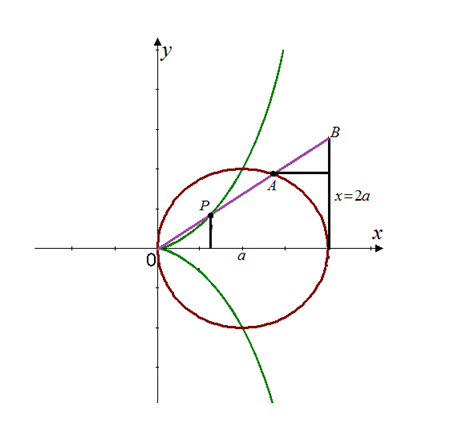
Single Variable Calculus: Concepts and Contexts, Enhanced Edition, Chapter 1, Problem 34RE , additional homework tip 5

Hence, the result is plotted.

Chapter 1, Problem 33RE

Chapter 1, Problem 1P

Chapter 1 Solutions

Single Variable Calculus: Concepts and Contexts, Enhanced Edition

Ch. 1.1 - The graph of a function f is given. (a) State the...Ch. 1.1 - The graphs of f and g are given. (a) State the...Ch. 1.1 - Figure 1 was recorded by an instrument operated by...Ch. 1.1 - Prob. 5E Ch. 1.1 - Determine whether the curve is the graph of a...Ch. 1.1 - Prob. 7E Ch. 1.1 - Prob. 8E Ch. 1.1 - Prob. 9E Ch. 1.1 - Prob. 10E Ch. 1.1 - Prob. 11E

Ch. 1.1 - Prob. 12E Ch. 1.1 - The graph shows the power consumption for a day in...Ch. 1.1 - Prob. 14E Ch. 1.1 - Prob. 15E Ch. 1.1 - Prob. 16E Ch. 1.1 - Sketch the graph of the amount of a particular...Ch. 1.1 - You place a frozen pie in an oven and bake it for...Ch. 1.1 - Prob. 19E Ch. 1.1 - Prob. 20E Ch. 1.1 - Prob. 21E Ch. 1.1 - Prob. 22E Ch. 1.1 - Prob. 23E Ch. 1.1 - Prob. 24E Ch. 1.1 - Prob. 25E Ch. 1.1 - Prob. 26E Ch. 1.1 - Prob. 27E Ch. 1.1 - Prob. 28E Ch. 1.1 - Prob. 29E Ch. 1.1 - Prob. 30E Ch. 1.1 - Prob. 31E Ch. 1.1 - Prob. 32E Ch. 1.1 - Prob. 33E Ch. 1.1 - Prob. 34E Ch. 1.1 - Prob. 35E Ch. 1.1 - Prob. 36E Ch. 1.1 - Prob. 37E Ch. 1.1 - Prob. 38E Ch. 1.1 - Prob. 39E Ch. 1.1 - Prob. 40E Ch. 1.1 - Prob. 41E Ch. 1.1 - Prob. 42E Ch. 1.1 - Prob. 43E Ch. 1.1 - Prob. 44E Ch. 1.1 - Prob. 45E Ch. 1.1 - Prob. 46E Ch. 1.1 - Prob. 47E Ch. 1.1 - Prob. 48E Ch. 1.1 - Find an expression for the function whose graph is...Ch. 1.1 - Prob. 50E Ch. 1.1 - Prob. 51E Ch. 1.1 - Prob. 52E Ch. 1.1 - Prob. 53E Ch. 1.1 - Prob. 54E Ch. 1.1 - Prob. 55E Ch. 1.1 - Prob. 56E Ch. 1.1 - Prob. 57E Ch. 1.1 - A Norman window has the shape of a rectangle...Ch. 1.1 - Prob. 59E Ch. 1.1 - Prob. 60E Ch. 1.1 - Prob. 61E Ch. 1.1 - Prob. 62E Ch. 1.1 - Prob. 63E Ch. 1.1 - Prob. 64E Ch. 1.1 - Prob. 65E Ch. 1.1 - Prob. 66E Ch. 1.1 - Prob. 67E Ch. 1.1 - Prob. 68E Ch. 1.1 - Prob. 69E Ch. 1.1 - Prob. 70E Ch. 1.1 - Prob. 71E Ch. 1.1 - Prob. 72E Ch. 1.1 - Prob. 73E Ch. 1.1 - Prob. 74E Ch. 1.2 - Classify each function as a power function, root...Ch. 1.2 - Prob. 2E Ch. 1.2 - Prob. 3E Ch. 1.2 - Prob. 4E Ch. 1.2 - Prob. 5E Ch. 1.2 - Prob. 6E Ch. 1.2 - Prob. 7E Ch. 1.2 - Prob. 8E Ch. 1.2 - Prob. 9E Ch. 1.2 - Prob. 10E Ch. 1.2 - Prob. 11E Ch. 1.2 - The manager of a weekend flea market knows from...Ch. 1.2 - Prob. 13E Ch. 1.2 - Prob. 14E Ch. 1.2 - Biologists have noticed that the chirping rate of...Ch. 1.2 - Prob. 16E Ch. 1.2 - Prob. 17E Ch. 1.2 - Prob. 18E Ch. 1.2 - Prob. 19E Ch. 1.2 - Prob. 20E Ch. 1.2 - Prob. 21E Ch. 1.2 - Prob. 22E Ch. 1.2 - Prob. 23E Ch. 1.2 - Prob. 24E Ch. 1.2 - Prob. 25E Ch. 1.2 - Prob. 26E Ch. 1.3 - Suppose the graph of f is given. Write equations...Ch. 1.3 - Prob. 2E Ch. 1.3 - The graph of y=f(x) is given. Match each equation...Ch. 1.3 - Prob. 4E Ch. 1.3 - Prob. 5E Ch. 1.3 - Prob. 6E Ch. 1.3 - Prob. 7E Ch. 1.3 - Prob. 8E Ch. 1.3 - Prob. 9E Ch. 1.3 - Prob. 10E Ch. 1.3 - Prob. 11E Ch. 1.3 - Prob. 12E Ch. 1.3 - Prob. 13E Ch. 1.3 - Prob. 14E Ch. 1.3 - Prob. 15E Ch. 1.3 - Prob. 16E Ch. 1.3 - Prob. 17E Ch. 1.3 - Prob. 18E Ch. 1.3 - Prob. 19E Ch. 1.3 - Prob. 20E Ch. 1.3 - Prob. 21E Ch. 1.3 - Prob. 22E Ch. 1.3 - Prob. 23E Ch. 1.3 - Prob. 24E Ch. 1.3 - The city of New Orleans is located at latitude...Ch. 1.3 - Prob. 26E Ch. 1.3 - Prob. 27E Ch. 1.3 - Prob. 28E Ch. 1.3 - Prob. 29E Ch. 1.3 - Prob. 30E Ch. 1.3 - Prob. 31E Ch. 1.3 - Prob. 32E Ch. 1.3 - Prob. 33E Ch. 1.3 - Prob. 34E Ch. 1.3 - Prob. 35E Ch. 1.3 - Prob. 36E Ch. 1.3 - Prob. 37E Ch. 1.3 - Prob. 38E Ch. 1.3 - Prob. 39E Ch. 1.3 - Prob. 40E Ch. 1.3 - Prob. 41E Ch. 1.3 - Prob. 42E Ch. 1.3 - Prob. 43E Ch. 1.3 - Prob. 44E Ch. 1.3 - Express the function in the form f g. 47. v(t) =...Ch. 1.3 - Prob. 46E Ch. 1.3 - Prob. 47E Ch. 1.3 - Prob. 48E Ch. 1.3 - Prob. 49E Ch. 1.3 - Prob. 50E Ch. 1.3 - Prob. 51E Ch. 1.3 - Use the given graphs of f and g to estimate the...Ch. 1.3 - Prob. 53E Ch. 1.3 - Prob. 54E Ch. 1.3 - A ship is at a speed of 30km/h parallel to a...Ch. 1.3 - Prob. 56E Ch. 1.3 - Prob. 57E Ch. 1.3 - The Heaviside function defined in Exercise 59 can...Ch. 1.3 - Prob. 59E Ch. 1.3 - Prob. 60E Ch. 1.3 - Prob. 61E Ch. 1.3 - Prob. 62E Ch. 1.3 - Prob. 63E Ch. 1.3 - Prob. 64E Ch. 1.4 - Prob. 1E Ch. 1.4 - Prob. 2E Ch. 1.4 - Prob. 3E Ch. 1.4 - Prob. 4E Ch. 1.4 - Prob. 5E Ch. 1.4 - Prob. 6E Ch. 1.4 - Prob. 7E Ch. 1.4 - Prob. 8E Ch. 1.4 - Prob. 9E Ch. 1.4 - Prob. 10E Ch. 1.4 - Prob. 11E Ch. 1.4 - Prob. 12E Ch. 1.4 - Prob. 13E Ch. 1.4 - Prob. 14E Ch. 1.4 - Prob. 15E Ch. 1.4 - Prob. 16E Ch. 1.4 - Prob. 17E Ch. 1.4 - Prob. 18E Ch. 1.4 - Prob. 19E Ch. 1.4 - Prob. 20E Ch. 1.4 - Prob. 21E Ch. 1.4 - Prob. 22E Ch. 1.4 - Prob. 23E Ch. 1.4 - Prob. 24E Ch. 1.4 - Prob. 25E Ch. 1.4 - Prob. 26E Ch. 1.4 - Prob. 27E Ch. 1.4 - Prob. 28E Ch. 1.4 - Prob. 29E Ch. 1.4 - Prob. 30E Ch. 1.4 - Prob. 31E Ch. 1.4 - Prob. 32E Ch. 1.4 - Prob. 33E Ch. 1.4 - Prob. 34E Ch. 1.4 - Prob. 35E Ch. 1.4 - Prob. 36E Ch. 1.4 - Prob. 37E Ch. 1.4 - Prob. 38E Ch. 1.5 - Use the Law of Exponents to rewrite and simplify...Ch. 1.5 - Use the Law of Exponents to rewrite and simplify...Ch. 1.5 - Prob. 3E Ch. 1.5 - Use the Law of Exponents to rewrite and simplify...Ch. 1.5 - Prob. 5E Ch. 1.5 - Prob. 6E Ch. 1.5 - Prob. 7E Ch. 1.5 - Prob. 8E Ch. 1.5 - Prob. 9E Ch. 1.5 - Prob. 10E Ch. 1.5 - Prob. 11E Ch. 1.5 - Prob. 12E Ch. 1.5 - Prob. 13E Ch. 1.5 - Prob. 14E Ch. 1.5 - Make a rough sketch of the graph of the function....Ch. 1.5 - Prob. 16E Ch. 1.5 - Prob. 17E Ch. 1.5 - Prob. 18E Ch. 1.5 - Prob. 19E Ch. 1.5 - Prob. 20E Ch. 1.5 - Prob. 21E Ch. 1.5 - Find the exponential function f(x) = Cbx whose...Ch. 1.5 - Prob. 23E Ch. 1.5 - Suppose you are offered a job that lasts one...Ch. 1.5 - Prob. 25E Ch. 1.5 - Prob. 26E Ch. 1.5 - Prob. 27E Ch. 1.5 - Prob. 28E Ch. 1.5 - Prob. 29E Ch. 1.5 - A bacteria culture starts with 500 bacteria and...Ch. 1.5 - The half-life of bismuth-210, 210Bi, is 5 days....Ch. 1.5 - Prob. 32E Ch. 1.5 - Prob. 33E Ch. 1.5 - Prob. 34E Ch. 1.5 - Prob. 35E Ch. 1.5 - Prob. 36E Ch. 1.6 - (a) What is a one-to-one function? (b) How can you...Ch. 1.6 - Prob. 2E Ch. 1.6 - Prob. 3E Ch. 1.6 - Prob. 4E Ch. 1.6 - A function is given by a table of values, a graph,...Ch. 1.6 - A function is given by a table of values, a graph,...Ch. 1.6 - Prob. 7E Ch. 1.6 - A function is given by a table of values, a graph,...Ch. 1.6 - Prob. 9E Ch. 1.6 - Prob. 10E Ch. 1.6 - Prob. 11E Ch. 1.6 - Prob. 12E Ch. 1.6 - Prob. 13E Ch. 1.6 - Prob. 14E Ch. 1.6 - Assume that f is a one-to-one function. (a) If...Ch. 1.6 - Prob. 16E Ch. 1.6 - Prob. 17E Ch. 1.6 - Prob. 18E Ch. 1.6 - Prob. 19E Ch. 1.6 - Prob. 20E Ch. 1.6 - Prob. 21E Ch. 1.6 - Prob. 22E Ch. 1.6 - Prob. 23E Ch. 1.6 - Prob. 24E Ch. 1.6 - Find a formula for the inverse of the function....Ch. 1.6 - Prob. 26E Ch. 1.6 - Prob. 27E Ch. 1.6 - Prob. 28E Ch. 1.6 - Prob. 29E Ch. 1.6 - Prob. 30E Ch. 1.6 - Prob. 31E Ch. 1.6 - Prob. 32E Ch. 1.6 - Prob. 33E Ch. 1.6 - Prob. 34E Ch. 1.6 - Prob. 35E Ch. 1.6 - Prob. 36E Ch. 1.6 - Prob. 37E Ch. 1.6 - Prob. 38E Ch. 1.6 - Prob. 39E Ch. 1.6 - Prob. 40E Ch. 1.6 - Prob. 41E Ch. 1.6 - Use Formula 10 to evaluate each logarithm correct...Ch. 1.6 - Prob. 43E Ch. 1.6 - Prob. 44E Ch. 1.6 - Prob. 45E Ch. 1.6 - Prob. 46E Ch. 1.6 - Prob. 47E Ch. 1.6 - Make a rough sketch of the graph of each function....Ch. 1.6 - Solve each equation for x. 51. (a) e74x=6 (b)...Ch. 1.6 - Prob. 50E Ch. 1.6 - Prob. 51E Ch. 1.6 - Prob. 52E Ch. 1.6 - Prob. 53E Ch. 1.6 - Prob. 54E Ch. 1.6 - Prob. 55E Ch. 1.6 - Prob. 56E Ch. 1.6 - Prob. 57E Ch. 1.6 - Prob. 58E Ch. 1.6 - Prob. 59E Ch. 1.6 - Prob. 60E Ch. 1.6 - Prob. 61E Ch. 1.6 - Prob. 62E Ch. 1.7 - Prob. 1E Ch. 1.7 - Prob. 2E Ch. 1.7 - Prob. 3E Ch. 1.7 - Prob. 4E Ch. 1.7 - Prob. 5E Ch. 1.7 - Prob. 6E Ch. 1.7 - Prob. 7E Ch. 1.7 - Prob. 8E Ch. 1.7 - Prob. 9E Ch. 1.7 - Prob. 10E Ch. 1.7 - Prob. 11E Ch. 1.7 - Prob. 12E Ch. 1.7 - Prob. 13E Ch. 1.7 - Prob. 14E Ch. 1.7 - Prob. 15E Ch. 1.7 - Prob. 16E Ch. 1.7 - Prob. 17E Ch. 1.7 - Prob. 18E Ch. 1.7 - Prob. 19E Ch. 1.7 - Prob. 20E Ch. 1.7 - Prob. 21E Ch. 1.7 - Prob. 22E Ch. 1.7 - Prob. 23E Ch. 1.7 - Prob. 24E Ch. 1.7 - Prob. 25E Ch. 1.7 - Prob. 26E Ch. 1.7 - Prob. 27E Ch. 1.7 - Prob. 28E Ch. 1.7 - Prob. 29E Ch. 1.7 - Prob. 30E Ch. 1.7 - Prob. 31E Ch. 1.7 - Prob. 32E Ch. 1.7 - Prob. 33E Ch. 1.7 - Prob. 34E Ch. 1.7 - Prob. 35E Ch. 1.7 - Prob. 36E Ch. 1.7 - Prob. 37E Ch. 1.7 - Prob. 38E Ch. 1.7 - Prob. 39E Ch. 1.7 - Prob. 40E Ch. 1.7 - Prob. 41E Ch. 1.7 - Prob. 42E Ch. 1.7 - Prob. 43E Ch. 1.7 - Prob. 44E Ch. 1.7 - Prob. 45E Ch. 1.7 - Prob. 46E Ch. 1 - Prob. 1RQ Ch. 1 - Prob. 2RQ Ch. 1 - Prob. 3RQ Ch. 1 - Prob. 4RQ Ch. 1 - Prob. 5RQ Ch. 1 - Prob. 6RQ Ch. 1 - Prob. 7RQ Ch. 1 - Determine whether the statement is true or false....Ch. 1 - Determine whether the statement is true or false....Ch. 1 - Prob. 10RQ Ch. 1 - Prob. 11RQ Ch. 1 - Prob. 12RQ Ch. 1 - (a) What is a function? What are its domain and...Ch. 1 - Discuss four ways of representing a function....Ch. 1 - (a) What is an even function? How can you tell if...Ch. 1 - Prob. 4RCC Ch. 1 - Prob. 5RCC Ch. 1 - Prob. 6RCC Ch. 1 - Prob. 7RCC Ch. 1 - Prob. 8RCC Ch. 1 - Suppose that f has domain A and g has domain B....Ch. 1 - Prob. 10RCC Ch. 1 - Prob. 11RCC Ch. 1 - Prob. 12RCC Ch. 1 - Prob. 13RCC Ch. 1 - Let f be the function whose graph is given. (a)...Ch. 1 - Prob. 2RE Ch. 1 - Prob. 3RE Ch. 1 - Prob. 4RE Ch. 1 - Prob. 5RE Ch. 1 - Prob. 6RE Ch. 1 - Prob. 7RE Ch. 1 - Prob. 8RE Ch. 1 - Suppose that the graph of .f is given. Describe...Ch. 1 - Prob. 10RE Ch. 1 - Prob. 11RE Ch. 1 - Prob. 12RE Ch. 1 - Prob. 13RE Ch. 1 - Prob. 14RE Ch. 1 - Prob. 15RE Ch. 1 - Prob. 16RE Ch. 1 - Prob. 17RE Ch. 1 - Prob. 18RE Ch. 1 - Prob. 19RE Ch. 1 - Prob. 20RE Ch. 1 - Prob. 22RE Ch. 1 - Prob. 23RE Ch. 1 - Prob. 24RE Ch. 1 - Prob. 25RE Ch. 1 - Prob. 26RE Ch. 1 - The half-life of palladium-100, 100Pd, is four...Ch. 1 - The population of a certain species in a limited...Ch. 1 - Prob. 29RE Ch. 1 - Prob. 30RE Ch. 1 - Prob. 31RE Ch. 1 - Prob. 32RE Ch. 1 - Prob. 33RE Ch. 1 - Prob. 34RE Ch. 1 - One of the legs of a right triangle has length 4...Ch. 1 - Prob. 2P Ch. 1 - Prob. 3P Ch. 1 - Prob. 4P Ch. 1 - Prob. 5P Ch. 1 - Prob. 6P Ch. 1 - Prob. 7P Ch. 1 - Prob. 8P Ch. 1 - Prob. 9P Ch. 1 - Prob. 10P Ch. 1 - Prob. 11P Ch. 1 - Prob. 12P Ch. 1 - Prob. 13P Ch. 1 - Prob. 14P Ch. 1 - Prob. 15P Ch. 1 - Prob. 16P Ch. 1 - Prob. 17P Ch. 1 - Prove that 1 + 3 + 5 + + (2n l ) = n2.Ch. 1 - Prob. 19P Ch. 1 - Prob. 20P

Knowledge Booster

$Calculus$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.

Find parametric equations for the set of all points P .

Concept explainers

Videos

Find parametric equations for the set of all points P<m:math><m:mi>P</m:mi></m:math> .

Answer to Problem 34RE

Explanation of Solution

Use the geometric description of the curve to draw a rough of the curve by hand.

Answer to Problem 34RE

Explanation of Solution

Chapter 1 Solutions

Find parametric equations for the set of all points $P$ .