
(a)
To sketch: The rough graph of the function
(a)
Explanation of Solution
The rough graph of
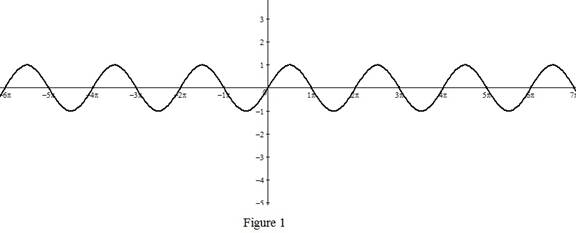
From Figure 1, it is observed that the sine function is defined on
(b)
To sketch: The rough graph of the function
(b)
Explanation of Solution
The rough graph of
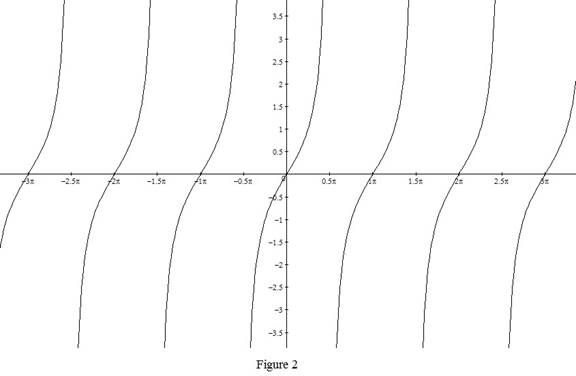
From Figure 2, it is observed that the tan function is undefined when cos x = 0 and is a periodic with period
(c)
To sketch: The rough graph of the function
(c)
Explanation of Solution
The rough graph of
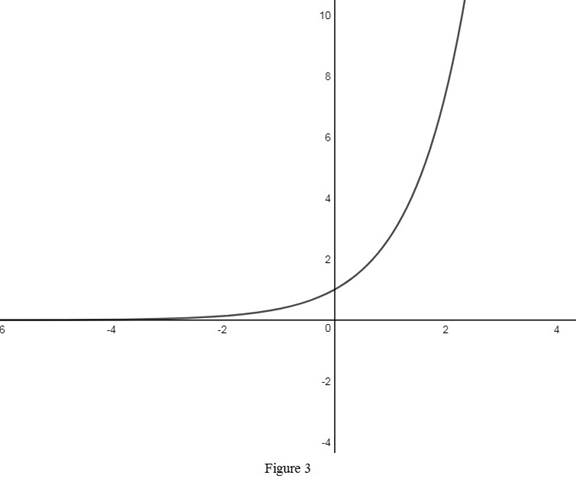
From Figure 3, it is observed that the exponential function is an increasing function with the domain
(d)
To sketch: The rough graph of the function
(d)
Explanation of Solution
The rough graph of
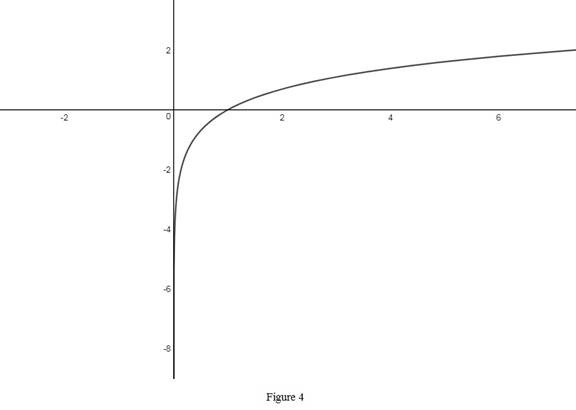
From Figure 4, it is observed that the logarithmic function is an increasing function with the domain
(e)
To sketch: The rough graph of the function
(e)
Explanation of Solution
The rough graph of
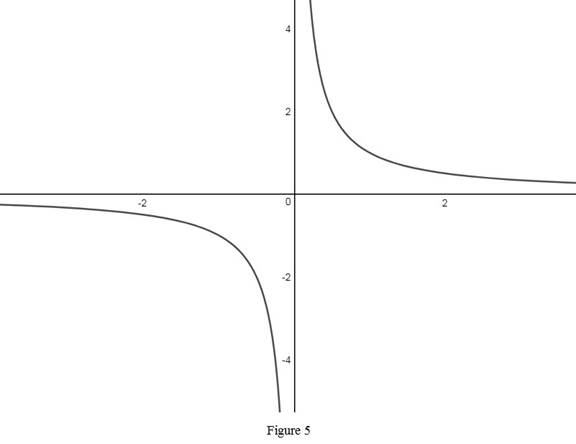
From Figure 5, it is observed that the reciprocal function is an hyperbola with x and y axes as its asymptotes.
(f)
To sketch: The rough graph of the function
(f)
Explanation of Solution
The rough graph of
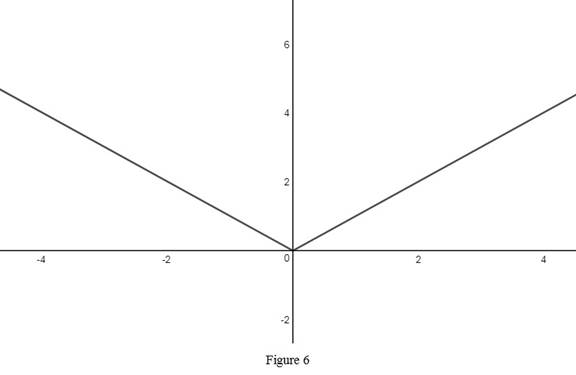
From Figure 6, it is observed that the range of an absolute function is positive y-axis.
(g)
To sketch: The rough graph of the function
(g)
Explanation of Solution
The rough graph of
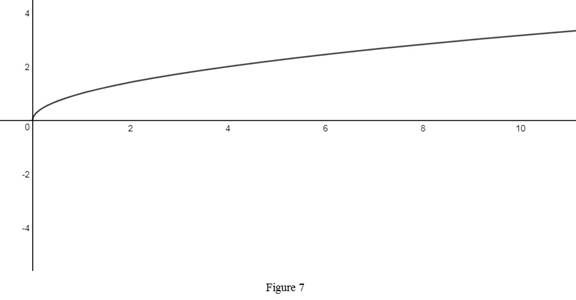
From Figure 7, it is observed that the range of the power function with the power
(h)
To sketch: The rough graph of the function
(h)
Explanation of Solution
The rough graph of
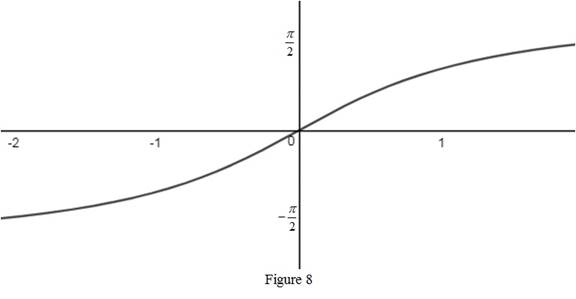
From Figure 8, it is observed that the domain of an inverse tan function is
Chapter 1 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





