Mechanics of Materials (MindTap Co...
Solutions
Mechanics of Materials (MindTap Co...
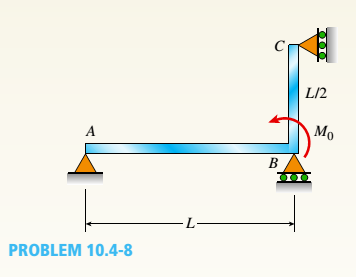
The continuous frame ABC has a pin support at /l, roller supports at B and C, and a rigid corner connection at B (see figure). Members AB and BC each have flexural rigidity EI. A moment M0acts counterclockwise at B, Note: Disregard axial deformations in member AB and consider only the effects of bending.
- Find all reactions of the frame.
Find the required new length of member BC in terms of L., so that
(a)
All the reactions of the frame.
Given Information:
The following figure is given with all relevant information,
Calculation:
Consider the following free body diagram,
Take equilibrium of horizontal forces as,
Take equilibrium of vertical forces as,
Take equilibrium of moments about B as,
The bending moment at distance x from A along AB in part AB is given by,
Use second order deflection differential equation,
Integrate above equation to get rotation as,
Integrate above equation to get rotation as,
The bending moment at distance x from B along BC in part BC is given by,
Use second order deflection differential equation,
  
(b)
Rotations at joints A, B and C.
(c)
Length of BC.
Chapter 10 Solutions
Additional Engineering Solutions
Find more solutions based on key concepts
Show solutions addA programmable indexing fixture creates a fourth axis called a ________ __________ that is similar to a rotary ...
Precision Machining Technology (MindTap Course List)
What is the purpose of having two accelerator pedal signals in an electronic throttle control system?
Automotive Technology: A Systems Approach (MindTap Course List)
The sieve analysis data for a granular' soil are given below. % passing 19 mm sieve = 100 % passing 4.75 mm sie...
Fundamentals of Geotechnical Engineering (MindTap Course List)
How does a secured bond differ from an unsecured bond?
Cornerstones of Financial Accounting
What is meant by the term business analytics? What other terms have been used for business analytics systems?
Principles of Information Systems (MindTap Course List)
Explain why the cost of ownership may be lower with a cloud database than with a traditional, company database.
Database Systems: Design, Implementation, & Management
Using the ERD from Problem 10, create the relational schema. (Create an appropriate collection of attributes fo...
Database Systems: Design, Implementation, & Management
What was the earliest reason for the use of cryptography?
Principles of Information Security (MindTap Course List)
Define the terms data warehouse, data mart, and data lakes and explain how they are different.
Fundamentals of Information Systems
Which PL/SQL command activates a cursor?
A Guide to SQL
Do research to find any professional organization or code of ethics associated with your current or desired fut...
Fundamentals of Information Systems
Repeat Problem 2.11 with the following data. 2.11 The grain-size characteristics of a soil are given in the fol...
Principles of Geotechnical Engineering (MindTap Course List)
Cobalt-chromium alloys, stainless steel, and titanium alloys are three common biomaterials that have been used ...
Engineering Fundamentals: An Introduction to Engineering (MindTap Course List)
Knowing that the two forces shown can be replaced by an equivalent force acting at O (no couple), determine P.
International Edition---engineering Mechanics: Statics, 4th Edition
Use a Web search engine to find a general encyclopedic article on agile approaches to an SDLC. You might use a ...
Management Of Information Security
Calorie (energy) and horsepower (power) are two non-SI units that you might see on occasion. A. Death Valley Na...
Fundamentals of Chemical Engineering Thermodynamics (MindTap Course List)
How many conductors enter the ceiling fan/light wall box?
EBK ELECTRICAL WIRING RESIDENTIAL
To increase generator voltage: (a) Should the resistance of the rheostat be increased or decreased? (b) What ch...
Electric Motor Control
What is an effective way to assess user requests for additional features and functions?
Systems Analysis and Design (Shelly Cashman Series) (MindTap Course List)
Explain in your own words how a jig works.
Solid Waste Engineering
Technician A says that a tap cuts external threads. Technician B says that a die cuts internal threads. Who is ...
Automotive Technology
ERP a. processing system in which the computer processes each transaction as it is entered b. application of hu...
Enhanced Discovering Computers 2017 (Shelly Cashman Series) (MindTap Course List)
Use LRFD and design the hearing stiffeners for the girder of Problem 10.7-4. Use Fy=50 ksi.
Steel Design (Activate Learning with these NEW titles from Engineering!)
