Principles of Economics 2e
2nd Edition
ISBN: 9781947172364
Author: Steven A. Greenlaw; David Shapiro
Publisher: OpenStax
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 10, Problem 21P
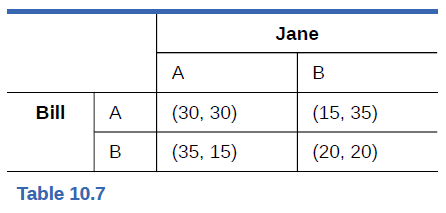
Jane and Bill are apprehended for a bank robbery. They are taken into separate rooms and questioned by the police about their involvement in the crime. The police tell them each that if they confess and turn the other person in, they will receive a fighter sentence. If they both confess, they will be each be sentenced to 30 years. If neither confesses, they will each receive a 20-year sentence. If only one confesses, the they will receive 15 years and the one who stayed silent will receive 35 years. Table 10.7 below represents the choices available to Jane and Bill. If Jane trusts Bill to stay silent, what should she do? If Jane thinks that Bill will confess, what should she do? Does Jane have a dominant strategy? Does Bill have a dominant strategy? A = Confess; B = Stay Silent. (Each results entry lists Jane’s sentence first (in years), and Bill’s sentence second.)
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
two players, a and b are playing an asymmetrical game. there are n points on the game board. each turn player a targets a pair of points and player b says whether those two points are connected or unconnected. a can target each pair only once and the game ends when all pairs have been targeted. player b wins if a point is connected with all other points on the very last turn, while player a wins if any point is connected with all other points on any turn but the very last one or if no point is connected to all other points after the last turn. for what values of n does either player have a winning strategy?
We have a group of three friends: Kramer, Jerry and Elaine. Kramer has a $10 banknote that he will auction off, and Jerry and Elaine will be bidding for it. Jerry and Elaine have to submit their bids to Kramer privately, both at the same time. We assume that both Jerry and Elaine only have $2 that day, and the available strategies to each one of them are to bid either$0, $1 or $2. Whoever places the highest bid, wins the $10 banknote. In case of a tie (that is, if Jerry and Elaine submit the same bid), each one of them gets $5. Regardless of who wins the auction, each bidder has to pay to Kramer whatever he or she bid.
Does this game have a Nash Equilibrium? (If not, why not? If yes, what is the Nash Equilibrium?)
We have a group of three friends: Kramer, Jerry and Elaine. Kramer has a $10 banknote that he will auction off, and Jerry and Elaine will be bidding for it. Jerry and Elaine have to submit their bids to Kramer privately, both at the same time. We assume that both Jerry and Elaine only have $2 that day, and the available strategies to each one of them are to bid either$0, $1 or $2. Whoever places the highest bid, wins the $10 banknote. In case of a tie (that is, if Jerry and Elaine submit the same bid), each one of them gets $5. Regardless of who wins the auction, each bidder has to pay to Kramer whatever he or she bid.
Does Jerry have any strictly dominant strategy? Does Elaine?
Chapter 10 Solutions
Principles of Economics 2e
Ch. 10 - Suppose that, due to a successful advertising...Ch. 10 - Continuing with the scenario in question 1, in the...Ch. 10 - Consider the curve in the figure below, which...Ch. 10 - Sometimes oligopolies in the same industry are...Ch. 10 - What is the relationship between product...Ch. 10 - How is the perceived demand curve for a...Ch. 10 - How does a monopolistic competitor choose its...Ch. 10 - How can a monopolistic competitor tell whether the...Ch. 10 - If the firms in a monopolistically competitive...Ch. 10 - Is a monopolistically competitive firm...
Ch. 10 - Will the firms in an oligopoly act more like a...Ch. 10 - Does each individual in a prisoners dilemma...Ch. 10 - What stops oligopolists from acting together as a...Ch. 10 - Aside from advertising, how can monopolistically...Ch. 10 - Make a case for why monopolistically competitive...Ch. 10 - Would you rather have efficiency or variety? That...Ch. 10 - Would you expect the kinked demand curve to be...Ch. 10 - When OPEC raised the price of oil dramatically in...Ch. 10 - Andreas Day Spa began to offer a relaxing...Ch. 10 - May and Raj me the only two growers who provide...Ch. 10 - Jane and Bill are apprehended for a bank robbery....
Additional Business Textbook Solutions
Find more solutions based on key concepts
Direct, indirect, fixed, and variable costs. California Tires manufactures two types of tires that it sells as ...
Horngren's Cost Accounting: A Managerial Emphasis (16th Edition)
Ravenna Candles recently purchased candleholders for resale in its shops. Which of the following costs would be...
Financial Accounting (12th Edition) (What's New in Accounting)
Identify whether ongoing transactions posted to the following accounts would normally have only debit entries (...
Principles of Accounting Volume 1
Prepare a production cost report and journal entries (Learning Objectives 4 5) Vintage Accessories manufacture...
Managerial Accounting (5th Edition)
What are the three major types of communication?
Principles of Management
Discussion Questions 1. What characteristics of the product or manufacturing process would lead a company to us...
Managerial Accounting (4th Edition)
Knowledge Booster
Similar questions
- Jane and Bill are apprehended for a bank robbery. They are taken into separate rooms and questioned by the police about their involvement in the crime. The police tell them each that if they confess and turn the other person in, they will receive a lighter sentence. If they both confess, they will each be sentenced to 30 years. If neither confesses, they will each receive a 20-year sentence. If only one confesses, the confessor will receive 15 years and the one who stayed silent will receive 35 years. The table below represents the choices available to Jane and Bill. If Jane trusts Bill to stay silent, what should she do? If Jane thinks that Bill will confess, what should she do? Does Jane have a dominant strategy? A = Confess; B = Stay Silent. (Each results entry lists Janes sentence first (in years), and Bill's sentence second.) A A (30,30) A B (35,15) B A (15, 35) B B (20, 20)arrow_forwardTwo travelers own an identical suitcase that contains identical antiques. The airline is liable for a maximum of $100 per suitcase. To determine how much to reimburse each traveler, the airline puts them in different rooms (so that they cannot communicate), and ask them to write down an amount (an integer number) between $2 and $100. If both write down the same number, the airline will reimburse both travelers that amount. However, if the two amounts are different, both travelers will be paid the lowest of the two numbers along with a bonus/malus: $2 extra will be paid to the traveler who wrote down the lower value and a $2 deduction will be taken from the person who wrote down the higher amount. What are the travelers’ best response functions? What are the Nash equilbria of the game? Are they Pareto efficient? Explain the intuition why.arrow_forwardPhil, Stu, and Doug are deciding which fraternity to pledge. They all assign a payoff of 5 to pledging Phi Gamma and a payoff of 4 to Delta Chi. The payoff from not pledging either house is 1. Phi Gamma and Delta Chi each have two slots. If all three of them happen to choose the same house, then the house will randomly choose which two are admitted. In that case, each has probability 2/3 of getting in and probability 1/3 of not pledging any house. If they do not all choose the same house, then all are admitted to the house they chose. Find a symmetric Nash equilibrium in mixed strategies.arrow_forward
- Jane and Bill are apprehended for a bank robbery. They are taken into separate rooms and questioned by the police about their involvement in the crime. The police tell them each that if they confess and turn the other person in, they will receive a lighter sentence. If they both confess, they will be each be sentenced to 30 years. If neither confesses, they will each receive a 20-year sentence. If only one confesses, the confessor will receive 15 years and the one who stayed silent will receive 35 years. Table 10.7 below represents the choices available to Jane and Bill. If Jane trusts Bill to stay silent, what should she do? If Jane thinks that Bill will confess, what should she do? Does Jane have a dominant strategy? Does Bill have a dominant strategy? A = Confess; B = Stay Silent. (Each results entry lists Jane’s sentence first (in years), and Bill's sentence second.)arrow_forwardJane and Bill are apprehended for a bank robbery. They are taken into separate rooms and questioned by the police about their involvement in the crime. The police tell them each that if they confess and turn the other person in, they will receive a lighter sentence. If they both confess, they will be each be sentenced to 30 years. If neither confesses, they will each receive a 20-year sentence. If only one confesses, the confessor will receive 15 years and the one who stayed silent will receive 35 years. The table below represents the choices available to Jane and Bill. If Jane trusts Bill to stay silent, what should she do? A = Confess; B = Stay Silent (Each results entry lists Janes's sentence first (in years), and Bill's sentence second.) Jane A B Bill A (30, 30) (15, 35) B (35, 15) (20, 20)arrow_forwardJane and Bill are apprehended for a bank robbery. They are taken into separate rooms and questioned by the police about their involvement in the crime. The police tell them each that if they confess and turn the other person in, they will receive a lighter sentence. If they both confess, they will be each be sentenced to 30 years. If neither confesses, they will each receive a 20-year sentence. If only one confesses, the confessor will receive 15 years and the one who stayed silent will receive 35 years. The table below represents the choices available to Jane and Bill. If Jane thinks that Bill will confess, what should she do? A = Confess; B = Stay Silent. (Each results entry lists Janes's sentence first (in years), and Bill's sentence second.)arrow_forward
- Jane and Bill are apprehended for a bank robbery. They are taken into separate rooms and questioned by the police about their involvement in the crime. The police tell them each that if they confess and turn the other person in, they will receive a lighter sentence. If they both confess, they will be each be sentenced to 30 years. If neither confesses, they will each receive a 20-year sentence. If only one confesses, the confessor will receive 15 years and the one who stayed silent will receive 35 years. The table below represents the choices available to Jane and Bill. Which criminal(s) have a dominate strategy to cheat? A = Confess; B = Stay Silent. (Each results entry lists Janes's sentence first (in years), and Bill's sentence second.) Jane A B Bill A (30, 30) (15, 35) B (35, 15) (20, 20) Question 3 options: Only Bill has a dominate strategy so he should cheat Only Jane has a dominate strategy so she should cheat Both Bill…arrow_forwardAssume the following game situation: If Player A plays UP and Player B plays LEFT then Player A gets $2 and Player B gets $4. If Player A plays UP and Player B plays RIGHT then Player A gets $3 and Player B gets $6. If Player A plays DOWN and Player B plays LEFT then Player A gets $5 and Player B gets $2. If Player A plays DOWN and Player B plays RIGHT then Player A gets $1 and Player B gets $1. What is the mixed strategy expected payout for Player B? 1 40/15 39/15 11/2arrow_forwardJohn and Paul are walking in the woods one day when suddenly an angry bear emerges from the underbrush. They each can do one of two things: run away or stand and fight. If one of them runs away and the other fights, then the one who ran will get away unharmed (payoff of 0) while the one who fights will be killed (payoff -100). If they both run, then the bear will chase down one of them and eat them to death but the other one will get away unharmed. Assuming they don't know which one will escape we will call this a payoff of -50 for both. If they BOTH fight, then they will successfully drive off the bear but they may be injured in the process (payoff -10). Construct a payoff matrix for this game and identify the pure strategy Nash equilibrium. (Indicate it with words not with a circle!)arrow_forward
- Consider a game with two players (Alice and Bob) and payoffffs Bob Bob s1 s2 Alice, s1 3, 3 0, 0 Alice, s2 0, 0 2, 2 In the equilibrium in the above game, Alice should (A) always choose the fifirst strategy s1; (B) choose the fifirst strategy s1 with probability 40% ; (C) choose the fifirst strategy s1 with probability 50% ; (D) choose the fifirst strategy s1 with probability 60% .arrow_forwardSamiyah and DeAndre decide to play the following game. They take turns choosing either 1, 2, or 3. As each number is chosen, it is added to the previously chosen numbers. The winner is the player who chooses a number that brings the cumulative number to 10. For example, if Samiyah chooses and DeAndre chooses 2 (so the cumulative number is 5) and Samiyah chooses 2 and DeAndre chooses 3 then DeAndre wins as his choice of 3 results in the sum equaling 10. Using SPNE, who wins?arrow_forwardYou and a good friend are supposed to meet in Paris, France. You know you have arranged to meet at either the Arc de Triomphe (AdT) or at the base of the Eiffel Tower (ET) but you cannot remember which and you cannot communicate with each other. You prefer the Arc de Triomphe. Your friend prefers the Eiffel Tower. But you both much prefer to be together rather than apart. If you and your friend each arrive at the Arc de Triomphe, your payoff is 12 and your friend’s payoff is 8. If you and your friend each arrive at the Eiffel Tower, you friend’s payoff is 12 but your payoff is 8. If you go to the Arc de Triomphe and your friend goes to the Eiffel Tower, your payoff is 5 and your friend’s payoff is 5 If you go to the Eiffel Tower and your friend goes to the Arc de Triomphe, your payoff is 3 and your friend’s payoff is 3. If it helps, you can think of these payoffs as units of enjoyment or utility you and your friend derive from the outcomes. (As you recall, while firms…arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Managerial Economics: Applications, Strategies an...EconomicsISBN:9781305506381Author:James R. McGuigan, R. Charles Moyer, Frederick H.deB. HarrisPublisher:Cengage Learning
Managerial Economics: A Problem Solving ApproachEconomicsISBN:9781337106665Author:Luke M. Froeb, Brian T. McCann, Michael R. Ward, Mike ShorPublisher:Cengage Learning
Managerial Economics: Applications, Strategies an...
Economics
ISBN:9781305506381
Author:James R. McGuigan, R. Charles Moyer, Frederick H.deB. Harris
Publisher:Cengage Learning
Managerial Economics: A Problem Solving Approach
Economics
ISBN:9781337106665
Author:Luke M. Froeb, Brian T. McCann, Michael R. Ward, Mike Shor
Publisher:Cengage Learning