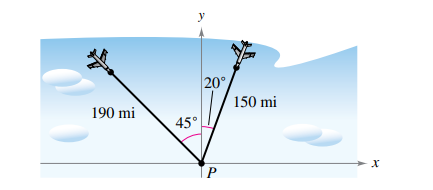
An air traffic controller spots two planes at the same altitude flying toward each other (see figure). Their flight paths are 20° and 315°. One plane is 150 miles from point P with a speed of 375 miles per hour. The other is 190 miles from point P with a speed of 450 miles per hour. (a) Find parametric equations for the path of each plane where t is the time in hours, with t = 0 corresponding to the time at which the air traffic controller spots the planes. (b) Use the result of part (a) to write the distance between the planes as a function of t. (c) Use a graphing utility to graph the function in part (b). When will the distance between the planes be minimum? If the planes must keep a separation of at least 3 miles, is the requirement met?
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 1 images




