College Algebra (MindTap Course List)
12th Edition
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:R. David Gustafson, Jeff Hughes
Chapter8: Sequences, Series, And Probability
Section8.6: Permutations And Combinations
Problem 5SC: In how many ways can 5 people stand in a line if one person demands to be first?
Related questions
Concept explainers
Vector Arithmetic
Vectors are those objects which have a magnitude along with the direction. In vector arithmetic, we will see how arithmetic operators like addition and multiplication are used on any two vectors. Arithmetic in basic means dealing with numbers. Here, magnitude means the length or the size of an object. The notation used is the arrow over the head of the vector indicating its direction.
Vector Calculus
Vector calculus is an important branch of mathematics and it relates two important branches of mathematics namely vector and calculus.
Question
Match the graphs of the parametric equations x=f(t) and y=g(t) in (a) - (d) with the parametric curves labeled I-IV
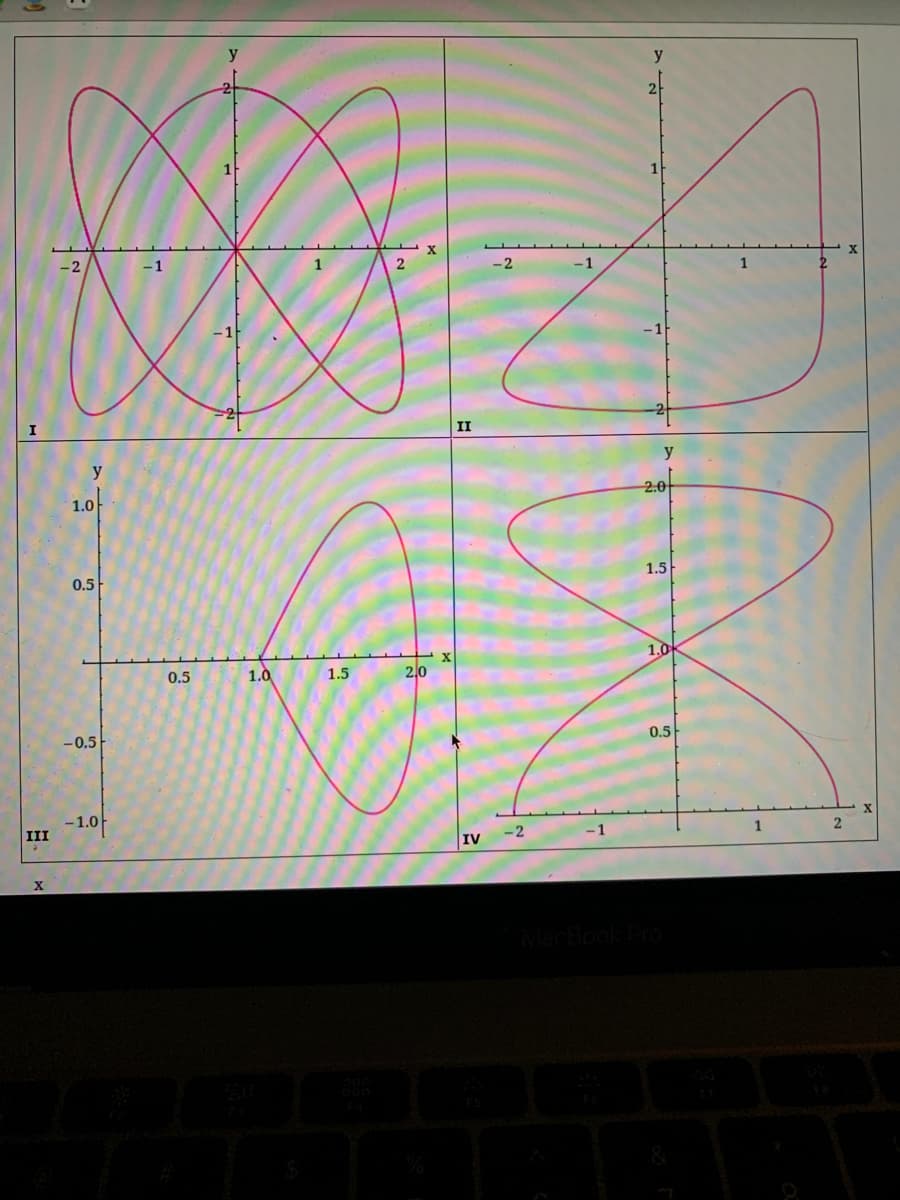
Transcribed Image Text:-1
2
-2
II
y
y
-2.아
1.0
1.5
0.5
0.5
1.0
1.5
2,0
0.5
-0,5
-1.0
1
III
IV
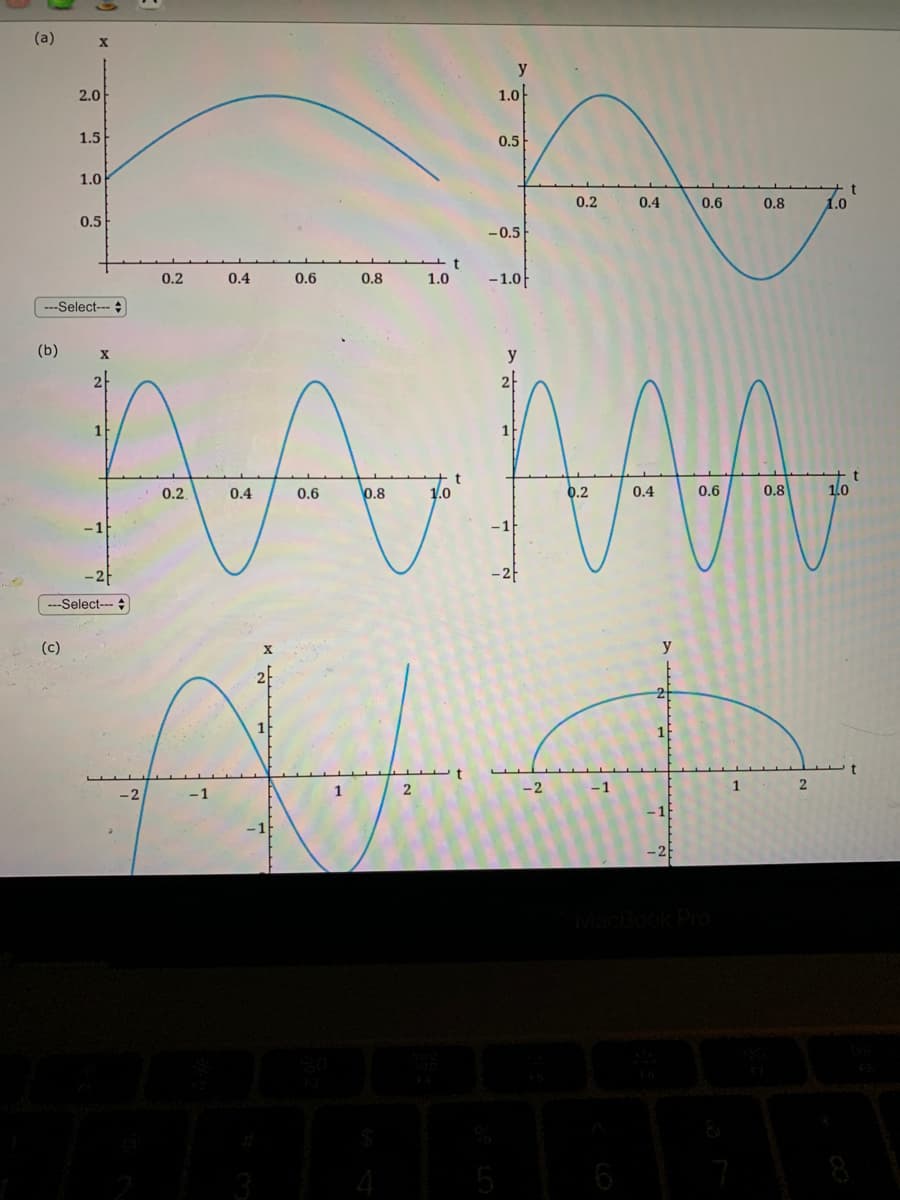
Transcribed Image Text:(a)
y
2.0
1.0
1.5
0.5
1.0
0.2
0.4
0.6
0.8
1.0
0.5
-0.5
0.2
0.4
0.6
0.8
1.0
-1.0F
---Select---
(b)
X
y
1
0.2.
0.4
0.6
0.8
V.O
0.2
0.4
0.6
0.8
1.0
-Select--- +
(c)
y
1
2
-2
-1
1
2
-1
5
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 5 steps

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Recommended textbooks for you

College Algebra (MindTap Course List)
Algebra
ISBN:
9781305652231
Author:
R. David Gustafson, Jeff Hughes
Publisher:
Cengage Learning

Algebra: Structure And Method, Book 1
Algebra
ISBN:
9780395977224
Author:
Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:
McDougal Littell

College Algebra (MindTap Course List)
Algebra
ISBN:
9781305652231
Author:
R. David Gustafson, Jeff Hughes
Publisher:
Cengage Learning

Algebra: Structure And Method, Book 1
Algebra
ISBN:
9780395977224
Author:
Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:
McDougal Littell