Trigonometric Identities
Trigonometry in mathematics deals with the right-angled triangle’s angles and sides. By trigonometric identities, we mean the identities we use whenever we need to express the various trigonometric functions in terms of an equation.
Inverse Trigonometric Functions
Inverse trigonometric functions are the inverse of normal trigonometric functions. Alternatively denoted as cyclometric or arcus functions, these inverse trigonometric functions exist to counter the basic trigonometric functions, such as sine (sin), cosine (cos), tangent (tan), cotangent (cot), secant (sec), and cosecant (cosec). When trigonometric ratios are calculated, the angular values can be calculated with the help of the inverse trigonometric functions.
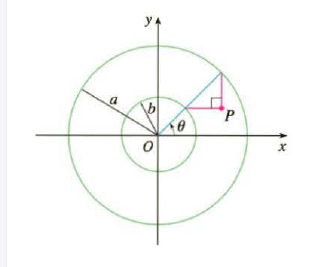
If a and b are fixed numbers, find parametric equations for the curve that consists of all possible positions of the point P in the figure, using the angle θ as the parameter. Then eliminate the parameter and identify the curve.
Trending now
This is a popular solution!
Step by step
Solved in 3 steps


