
Mathematical Applications for the Management, Life, and Social Sciences
11th Edition
ISBN: 9781305108042
Author: Ronald J. Harshbarger, James J. Reynolds
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
Chapter 10.1, Problem 45E
To determine
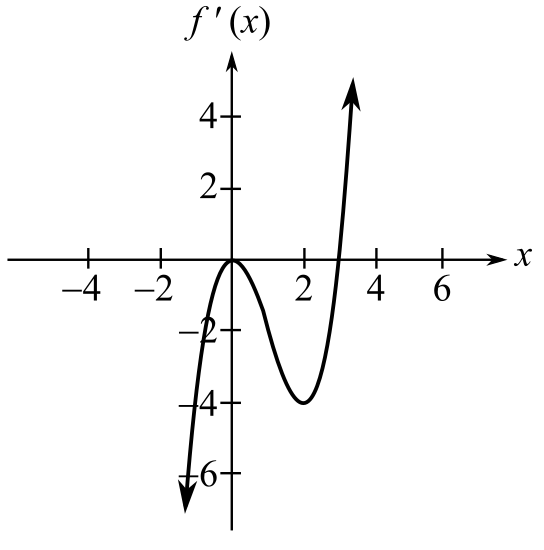
The intervals of x-values where the function derivative
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Chapter 10 Solutions
Mathematical Applications for the Management, Life, and Social Sciences
Ch. 10.1 - 1. The x- values of critical points are found...Ch. 10.1 - Prob. 2CPCh. 10.1 - Prob. 3CPCh. 10.1 - Prob. 4CPCh. 10.1 - In Problems 1 and 2, use the indicated points on...Ch. 10.1 - In Problems 1 and 2, use the indicated points on...Ch. 10.1 - 3. Use the graph of in Problem 1 to identify at...Ch. 10.1 - 4. Use the graph of in Problem 2 to identify at...Ch. 10.1 - In Problems 5 and 6, use the sign diagram for to...Ch. 10.1 - In Problems 5 and 6, use the sign diagram for to...
Ch. 10.1 - In Problems 7-10, (a) find the critical values of...Ch. 10.1 - In Problems 7-10, (a) find the critical values of...Ch. 10.1 - In Problems 7-10, (a) find the critical values of...Ch. 10.1 - In Problems 7-10, (a) find the critical values of...Ch. 10.1 - For each function and graph in Problems 11-14
(a)...Ch. 10.1 - Prob. 12ECh. 10.1 - Prob. 13ECh. 10.1 - Prob. 14ECh. 10.1 - For each function in Problems 15-20
(a) find
(b)...Ch. 10.1 - For each function in Problems 15-20
(a) find
(b)...Ch. 10.1 - For each function in Problems 15-20
(a) find
(b)...Ch. 10.1 - For each function in Problems 15-20
(a) find
(b)...Ch. 10.1 - Prob. 19ECh. 10.1 - Prob. 20ECh. 10.1 - Prob. 21ECh. 10.1 - For each function and graph in Problems 21-24
(a)...Ch. 10.1 - Prob. 23ECh. 10.1 - Prob. 24ECh. 10.1 - For each function in Problems 25-30, find the...Ch. 10.1 - Prob. 26ECh. 10.1 - Prob. 27ECh. 10.1 - For each function in Problems 25-30, find the...Ch. 10.1 - Prob. 29ECh. 10.1 - Prob. 30ECh. 10.1 - Prob. 31ECh. 10.1 - Prob. 32ECh. 10.1 - Prob. 33ECh. 10.1 - In Problems 31-36, both a function and its...Ch. 10.1 - Prob. 35ECh. 10.1 - In Problems 31-36, both a function and its...Ch. 10.1 - Prob. 37ECh. 10.1 - Prob. 38ECh. 10.1 - Prob. 39ECh. 10.1 - Prob. 40ECh. 10.1 - Prob. 41ECh. 10.1 - Prob. 42ECh. 10.1 - Prob. 43ECh. 10.1 - Prob. 44ECh. 10.1 - Prob. 45ECh. 10.1 - In each of Problems 43-46, a graph of is given....Ch. 10.1 - Prob. 47ECh. 10.1 - Prob. 48ECh. 10.1 - 49. Advertising and sales Suppose that the daily...Ch. 10.1 - 50. Pricing and sales Suppose that a chain of auto...Ch. 10.1 - 51. Productivity A time study showed that, on...Ch. 10.1 - 52. Production Analysis of daily output of a...Ch. 10.1 - 53. Production costs Suppose that the average...Ch. 10.1 - 54. Average costs Suppose the average costs of a...Ch. 10.1 - 55. Marginal revenue Suppose the weekly marginal...Ch. 10.1 - 56. Earnings Suppose that the rate of change of...Ch. 10.1 - 57. Revenue The weekly revenue of a certain...Ch. 10.1 - 58. Medication Suppose that the concentration C of...Ch. 10.1 - Prob. 59ECh. 10.1 - 60. Medication The number of milligrams x of a...Ch. 10.1 - 61. Worldwide cell phone subscriberships In 2013,...Ch. 10.1 - 62. Economic dependency ratio The economic...Ch. 10.1 - Prob. 63ECh. 10.1 - 64. Modeling Energy from crude oil The table shows...Ch. 10.1 - Prob. 65ECh. 10.2 - 1. If then is concave__________.
Ch. 10.2 - 2. At what value of x does the graph have a point...Ch. 10.2 - 3. On the graph below, locate any points of...Ch. 10.2 - 4. Determine whether the following is true or...Ch. 10.2 - Prob. 1ECh. 10.2 - Prob. 2ECh. 10.2 - In Problems 5-10, use the indicated x-values on...Ch. 10.2 - In Problems 5-10, use the indicated x-values on...Ch. 10.2 - In Problems 5-10, use the indicated x-values on...Ch. 10.2 - In Problems 5-10, use the indicated x-values on...Ch. 10.2 - In Problems 5-10, use the indicated x-values on...Ch. 10.2 - Prob. 8ECh. 10.2 - Prob. 9ECh. 10.2 - Prob. 10ECh. 10.2 - In Problems 11-14, a function and its graph are...Ch. 10.2 - Prob. 12ECh. 10.2 - Prob. 13ECh. 10.2 - Prob. 14ECh. 10.2 - Prob. 15ECh. 10.2 - Prob. 16ECh. 10.2 - Find the relative maxima, relative minima, and...Ch. 10.2 - Find the relative maxima, relative minima, and...Ch. 10.2 - Prob. 19ECh. 10.2 - Prob. 20ECh. 10.2 - Prob. 21ECh. 10.2 - Prob. 22ECh. 10.2 - Prob. 23ECh. 10.2 - Prob. 24ECh. 10.2 - Prob. 25ECh. 10.2 - Prob. 26ECh. 10.2 - In Problems 29 and 30, use the graph shown in the...Ch. 10.2 - In Problems 29 and 30, use the graph shown in the...Ch. 10.2 - In Problems 31 and 32, a graph is given. Tell...Ch. 10.2 - Prob. 30ECh. 10.2 - Prob. 31ECh. 10.2 - Prob. 32ECh. 10.2 - Prob. 33ECh. 10.2 - Prob. 34ECh. 10.2 - 37. Production Suppose that the total number of...Ch. 10.2 - 38. Poiscuille's law—velocity of blood According...Ch. 10.2 - 39. Advertising and sales—diminishing returns...Ch. 10.2 - 40. Oxygen purity—diminishing returns Suppose that...Ch. 10.2 - Prob. 39ECh. 10.3 - 1. True or false: If is the total revenue...Ch. 10.3 - Prob. 2CPCh. 10.3 - Prob. 3CPCh. 10.3 - Prob. 4CPCh. 10.3 - Prob. 1ECh. 10.3 - Prob. 2ECh. 10.3 - In Problems 1-6, find the absolute maxima and...Ch. 10.3 - 7. (a) If the total revenue function for a hammer...Ch. 10.3 - 8. (a) If the total revenue function for a blender...Ch. 10.3 - 9. If the total revenue function for a computer is...Ch. 10.3 - 10. A firm has total revenues given by
for x...Ch. 10.3 - 11. An agency charges $100 per person for a trip...Ch. 10.3 - 12. A company handles an apartment building with...Ch. 10.3 - 13. A cable TV company has 4000 customers paying...Ch. 10.3 - 14. If club members charge $5 admission to a...Ch. 10.3 - Prob. 13ECh. 10.3 - 16. For the revenue function given by
(a) find...Ch. 10.3 - 17. If the total cost function for a lamp is ...Ch. 10.3 - 18. If the total cost function for a product is ...Ch. 10.3 - 19. If the total cost function for a product is ...Ch. 10.3 - Prob. 18ECh. 10.3 - 21. If the total cost function for a product is ...Ch. 10.3 - 22. If the total cost function for a product is ...Ch. 10.3 - 23. For the cost function , show that average...Ch. 10.3 - 24. For the cost function , show that average...Ch. 10.3 - The graphs in Problems 25 and 26 show total cost...Ch. 10.3 - Prob. 24ECh. 10.3 - 27. If the profit function for a product is ...Ch. 10.3 - 28. If the profit function for a commodity is ...Ch. 10.3 - 29. A manufacturer estimates that its product can...Ch. 10.3 - 30. A product can be produced at a total cost ...Ch. 10.3 - 31. A firm can produce only 1000 units per month....Ch. 10.3 - 32. A firm can produce 100 units per week. If its...Ch. 10.3 - 33. A company handles an apartment building with...Ch. 10.3 - 34. A travel agency will plan a tour for groups of...Ch. 10.3 - 35. A firm has monthly average costs, in dollars,...Ch. 10.3 - 36. A small business has weekly average costs, in...Ch. 10.3 - 37. The weekly demand function for x units of a...Ch. 10.3 - 38. The monthly demand function for x units of a...Ch. 10.3 - 39. The monthly demand function for a product sold...Ch. 10.3 - 40. The monthly demand function for x units of a...Ch. 10.3 - 41. An industry with a monopoly on a product has...Ch. 10.3 - 42. A large corporation with monopolistic control...Ch. 10.3 - 43. Coastal Soda Sales has been granted exclusive...Ch. 10.3 - Prob. 47ECh. 10.3 - Prob. 48ECh. 10.3 - Prob. 49ECh. 10.4 - Suppose we want to find the minimum value of and...Ch. 10.4 - Prob. 2CPCh. 10.4 - Prob. 3CPCh. 10.4 - 1. Return to sales The manufacturer of GRIPPER...Ch. 10.4 - 2. Projectiles A ball thrown into the air from a...Ch. 10.4 - 3. Profit The profit per acre from a grove of...Ch. 10.4 - 4. Reaction rates The velocity v of an...Ch. 10.4 - 5. Productivity Analysis of daily output of a...Ch. 10.4 - 6. Productivity A time study showed that, on...Ch. 10.4 - Prob. 7ECh. 10.4 - 8. Production costs Suppose that the monthly cost...Ch. 10.4 - Prob. 9ECh. 10.4 - Medication For Problems 9 and 10, consider that...Ch. 10.4 - 11. Advertising and sales An inferior product with...Ch. 10.4 - Prob. 12ECh. 10.4 - 13. News impact Suppose that the percent p (as a...Ch. 10.4 - 14. Candidate recognition Suppose that in an...Ch. 10.4 - 15. Minimum fence Two equal rectangular lots are...Ch. 10.4 - 16. Minimum fence The running yard for a dog...Ch. 10.4 - Minimum cost A rectangular field with one side...Ch. 10.4 - Prob. 18ECh. 10.4 - 19. Optimization at a fixed cost A rectangular...Ch. 10.4 - Minimum cost A kennel of 640 square feet is to be...Ch. 10.4 - Minimum cost The base of a rectangular box is to...Ch. 10.4 - Prob. 22ECh. 10.4 - 23. Inventory cost model Suppose that a company...Ch. 10.4 - Inventory cost model Suppose that a company needs...Ch. 10.4 - Inventory cost model A company needs 150,000 items...Ch. 10.4 - Inventory cost model A company needs 450,000 items...Ch. 10.4 - 27. Volume A rectangular box with a square base is...Ch. 10.4 - Prob. 28ECh. 10.4 - 29. Revenue The owner of an orange grove must...Ch. 10.4 - 30. Minimum material
(a) A box with an open top...Ch. 10.4 - 31. Minimum cost A printer has a contract to print...Ch. 10.4 - 32. Shortest time A vacationer on an island 8...Ch. 10.4 - Prob. 33ECh. 10.5 - Prob. 1CPCh. 10.5 - Prob. 2CPCh. 10.5 - In Problems 1-4, a function and its graph are...Ch. 10.5 - Prob. 2ECh. 10.5 - Prob. 3ECh. 10.5 - Prob. 4ECh. 10.5 - Prob. 5ECh. 10.5 - Prob. 6ECh. 10.5 - Prob. 7ECh. 10.5 - Prob. 8ECh. 10.5 - Prob. 9ECh. 10.5 - Prob. 10ECh. 10.5 - Prob. 11ECh. 10.5 - Prob. 12ECh. 10.5 - Prob. 13ECh. 10.5 - Prob. 14ECh. 10.5 - Prob. 15ECh. 10.5 - Prob. 16ECh. 10.5 - Prob. 17ECh. 10.5 - Prob. 18ECh. 10.5 - Prob. 19ECh. 10.5 - In Problems 19-24, a function and its first and...Ch. 10.5 - Prob. 21ECh. 10.5 - Prob. 22ECh. 10.5 - Prob. 23ECh. 10.5 - Prob. 24ECh. 10.5 - Prob. 25ECh. 10.5 - Prob. 26ECh. 10.5 - Prob. 27ECh. 10.5 - Prob. 28ECh. 10.5 - Prob. 29ECh. 10.5 - Prob. 30ECh. 10.5 - Prob. 31ECh. 10.5 - For each function in Problems 29-34, complete the...Ch. 10.5 - Prob. 33ECh. 10.5 - Prob. 34ECh. 10.5 - Prob. 35ECh. 10.5 - Prob. 36ECh. 10.5 - 37. Revenue A recently released film has its...Ch. 10.5 - Prob. 38ECh. 10.5 - Prob. 39ECh. 10.5 - 40. Profit An entrepreneur starts new companies...Ch. 10.5 - 41. Productivity The figure is a typical graph of...Ch. 10.5 - Prob. 42ECh. 10.5 - 43. Females in the workforce For selected years...Ch. 10 - In Problems 1-4, find all critical points and...Ch. 10 - Prob. 2RECh. 10 - Prob. 3RECh. 10 - Prob. 4RECh. 10 - Prob. 5RECh. 10 - Prob. 6RECh. 10 - Prob. 7RECh. 10 - Prob. 8RECh. 10 - Prob. 9RECh. 10 - Prob. 10RECh. 10 - Prob. 11RECh. 10 - Prob. 12RECh. 10 - Prob. 13RECh. 10 - Prob. 14RECh. 10 - Prob. 15RECh. 10 - Prob. 16RECh. 10 - Prob. 17RECh. 10 - Prob. 18RECh. 10 - Prob. 19RECh. 10 - Prob. 20RECh. 10 - Prob. 21RECh. 10 - Prob. 22RECh. 10 - Prob. 23RECh. 10 - Prob. 24RECh. 10 - Prob. 25RECh. 10 - Prob. 26RECh. 10 - Prob. 27RECh. 10 - Prob. 28RECh. 10 - Prob. 29RECh. 10 - Prob. 30RECh. 10 - Prob. 31RECh. 10 - Prob. 32RECh. 10 - Prob. 33RECh. 10 - Prob. 34RECh. 10 - Prob. 35RECh. 10 - Prob. 36RECh. 10 - Prob. 37RECh. 10 - 38. Productivity—diminishing returns Suppose the...Ch. 10 - Prob. 39RECh. 10 - Prob. 40RECh. 10 - Prob. 41RECh. 10 - Prob. 42RECh. 10 - Prob. 43RECh. 10 - Prob. 44RECh. 10 - 45. Reaction to a drug The reaction R to an...Ch. 10 - Prob. 46RECh. 10 - 47. Population Population estimates show that the...Ch. 10 - Prob. 48RECh. 10 - 49. Product design A playpen manufacturer wants to...Ch. 10 - Prob. 50RECh. 10 - Prob. 51RECh. 10 - Prob. 52RECh. 10 - 53. Inventory cost model A company needs to...Ch. 10 - Prob. 54RECh. 10 - Prob. 55RECh. 10 - Prob. 1TCh. 10 - Prob. 2TCh. 10 - Prob. 3TCh. 10 - Prob. 4TCh. 10 - Prob. 5TCh. 10 - Prob. 6TCh. 10 - Prob. 7TCh. 10 - Prob. 8TCh. 10 - 9. Use the following graph of y = f(x) and the...Ch. 10 - Prob. 10TCh. 10 - Prob. 11TCh. 10 - Prob. 12TCh. 10 - 13. The revenue function for a product is dollars...Ch. 10 - Prob. 14TCh. 10 - 15. A firm sells 100 TVs per month at $300 each,...Ch. 10 - 16. An open-top box is made by cutting squares...Ch. 10 - Prob. 17T
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Recommended textbooks for you
 Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education
Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
 Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON
Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning,
Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning, Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education
Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education

Discrete Mathematics and Its Applications ( 8th I...
Math
ISBN:9781259676512
Author:Kenneth H Rosen
Publisher:McGraw-Hill Education

Mathematics for Elementary Teachers with Activiti...
Math
ISBN:9780134392790
Author:Beckmann, Sybilla
Publisher:PEARSON


Thinking Mathematically (7th Edition)
Math
ISBN:9780134683713
Author:Robert F. Blitzer
Publisher:PEARSON

Discrete Mathematics With Applications
Math
ISBN:9781337694193
Author:EPP, Susanna S.
Publisher:Cengage Learning,

Pathways To Math Literacy (looseleaf)
Math
ISBN:9781259985607
Author:David Sobecki Professor, Brian A. Mercer
Publisher:McGraw-Hill Education
Finding Local Maxima and Minima by Differentiation; Author: Professor Dave Explains;https://www.youtube.com/watch?v=pvLj1s7SOtk;License: Standard YouTube License, CC-BY