9. х — Vг, у — 1 -1 y
Vector Arithmetic
Vectors are those objects which have a magnitude along with the direction. In vector arithmetic, we will see how arithmetic operators like addition and multiplication are used on any two vectors. Arithmetic in basic means dealing with numbers. Here, magnitude means the length or the size of an object. The notation used is the arrow over the head of the vector indicating its direction.
Vector Calculus
Vector calculus is an important branch of mathematics and it relates two important branches of mathematics namely vector and calculus.
#9 2d
(a) Sketch the curve by using the parametric equations to plot
points. Indicate with an arrow the direction in which the curve
is traced as t increases.
(b) Eliminate the parameter to find a Cartesian equation of the
curve.
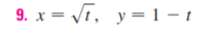
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 1 images








