
Concept explainers
The graphs of f and g are given.
(a) State the values of f(‒4) and g(3).
(b) For what values of x is f(x) = g(x)?
(c) Estimate the solution of the equation .f(x) = ‒1.
(d) On what interval is f decreasing?
(c) State the domain and range of f.
(f) State the domain and range of g.
(a)
The value of
Answer to Problem 2E
The value of
Explanation of Solution
Given:
Plot the points in the given graph as shown below in Figure 1.
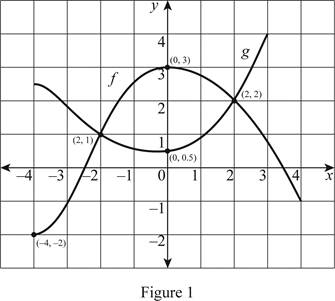
Calculation:
In Figure 1, x-axis represents the values of x and y-axis represents the values of
From Figure 1, it is noticeable that the point
Therefore,
(b)
The values of x if
Answer to Problem 2E
At
Explanation of Solution
Observe that the curves f and g are intersecting at two points
Therefore, the value of
(c)
The value of x if
Answer to Problem 2E
At
Explanation of Solution
From Figure 1, it is obvious that the points
If
That is, if
Therefore, the values of x = −3, 4 when
(d)
The decreasing interval of f.
Answer to Problem 2E
The decreasing interval of f is
Explanation of Solution
From Figure 1, it is noticeable that the curve f is decreasing from 3 to −1 between x = 0 and
Therefore, the decreasing interval of f is
(e)
The domain and range of f.
Answer to Problem 2E
The domain of f is
Explanation of Solution
Since the domain of a function is the set of all x values of the graph, the domain is
Thus, the domain of the function f is
Since, the range of a function is the set of all y values of the graph, the range is
Thus, the range of the function f is
(f)
The domain and range of g.
Answer to Problem 2E
The domain of g is
Explanation of Solution
Since, the domain of a function is the set of all x values of the graph, the domain is
Thus, the domain of the function g is
Since, the range of a function is the set of all y values of the graph, the range is
Thus, the range of the function g is
Chapter 1 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
Additional Math Textbook Solutions
Calculus 2012 Student Edition (by Finney/Demana/Waits/Kennedy)
Finite Mathematics and Calculus with Applications (10th Edition)
Calculus: Early Transcendentals (3rd Edition)
Precalculus
University Calculus: Early Transcendentals (4th Edition)
Calculus: Early Transcendentals (2nd Edition)
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





