
Volume
(a) Find the volume of the solid bounded below by the paraboloid
and above by the plane
(b) Find the volume of the solid bounded below by the elliptic paraboloid
and above by the plane
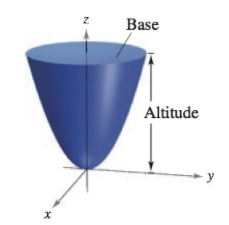
(c) Show that the volume of the solid in part (b) is equal to one-half the product of the area of the base times the altitude, as shown in the figure.
Want to see the full answer?
Check out a sample textbook solution
Chapter 11 Solutions
Calculus
- Surface area of a partial cylinder Find the surface area of the cylinder{(r, θ): r = 4, 0 ≤ θ ≤ 2π} between the planes z = 0 and z = 16 - 2x (excludingthe top and bottom surfaces).arrow_forwardFind the volumes of the solids The solid lies between planes perpendicular to the x-axis at x = 0 and x = 1. The cross-sections perpendicular to the x-axis between these planes are circular disks whose diameters run from the parabola y = x2 to the parabola y = √x.arrow_forwardMultivariable calc Find the volume of the solid enclosed by the paraboloid z = x 2 + 3y 2 and the planes x = 0, y = 4, y = x, z = 0.arrow_forward
- a. Center of mass Find the center of mass of a solid of constant density bounded below by the paraboloid z = x2 + y2 and above by the plane z = 4. b. Find the plane z = c that divides the solid into two parts of equal volume. This plane does not pass through the center of mass.arrow_forwardVolumes of solids Use a triple integral to find the volume of thefollowing solid. The wedge above the xy-plane formed when the cylinder x2 + y2 = 4 is cutby the planes z = 0 and y = -z.arrow_forwardFind the volumes of the solid...................The solid lies between planes perpendicular to the x-axis at x = -1 and x = 1. The cross-sections perpendicular to the x-axis are circular disks whose diameters run from the parabola y = x2 to the parabola y = 2 - x^2.arrow_forward
- Volume of the solid when R is revolved about the y-axis Y=x Y=7x Y=28arrow_forwardVolumes of solids Use a triple integral to find the volume of thefollowing solid. The solid in the first octant bounded by the plane2x + 3y + 6z = 12 and the coordinate planesarrow_forwardMass of a solid paraboloid Find the mass of the solid D bounded bythe paraboloid z = 4 - r2 and the plane z = 0 (see figure), where the density of the solid, given in cylindrical coordinates, is ƒ(r, θ, z) = 5 - z (heavy near the base and light near the vertex).arrow_forward
- find a parametrization of the surface. 1.The upper portion cut from the sphere x2 + y2 + z2 = 8 by the plane z =-2 2. Parabolic cylinder between planes The surface cut from the parabolic cylinder z = 4 - y2 by the planes x = 0, x = 2, and z = 0arrow_forwardFind the volumes of the solids The base of the solid is the region bounded by the parabola y2 = 4x and the line x = 1 in the xy-plane. Each cross-section perpendicular to the x-axis is an equilateral triangle with one edge in the plane. (The triangles all lie on the same side of the plane.)arrow_forwardMass of a box A solid box D is bounded by the planes x = 0, x = 3,y = 0, y = 2, z = 0, and z = 1. The density of the box decreases linearly in the positive z-direction and is given by ƒ(x, y, z) = 2 - z. Find the mass of the box.arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





