Use a graph of the sequence to decide whether the sequence is convergent or divergent. If the sequence is convergent, guess the value of the limit from the graph and then prove your guess. If it diverges write NONE. a, = 3/ñsin () lim a, =
Use a graph of the sequence to decide whether the sequence is convergent or divergent. If the sequence is convergent, guess the value of the limit from the graph and then prove your guess. If it diverges write NONE. a, = 3/ñsin () lim a, =
Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter10: Sequences, Series, And Probability
Section10.2: Arithmetic Sequences
Problem 64E
Related questions
Topic Video
Question
Use a graph of the sequence to decide whether the sequence is convergent or divergent. If the sequence is convergent, guess the value of the limit from the graph and then prove your guess. If it diverges write NONE.
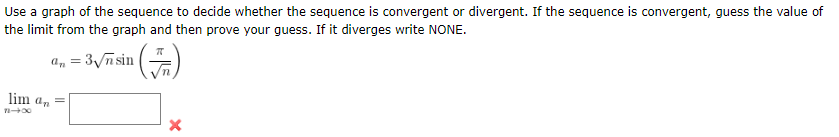
Transcribed Image Text:Use a graph of the sequence to decide whether the sequence is convergent or divergent. If the sequence is convergent, guess the value of
the limit from the graph and then prove your guess. If it diverges write NONE.
a, = 3/ñsin ()
lim a, =
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 4 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Recommended textbooks for you

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

College Algebra
Algebra
ISBN:
9781305115545
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

College Algebra
Algebra
ISBN:
9781305115545
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning